En este tema
Gráfica de probabilidad para datos originales y transformados
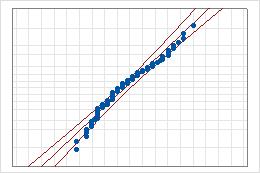
- Línea intermedia
- El percentil esperado de la distribución con base en estimaciones del parámetro de probabilidad máxima.
- Líneas de bordes de confianza
- Una línea izquierda curva indica los bordes inferiores de los intervalos de confianza para los percentiles. Una línea derecha curva indica los bordes superiores de los intervalos de confianza para los percentiles.
Interpretación
Utilice las gráficas de probabilidad normal para evaluar el grado en que los datos originales y transformados siguen la distribución normal.
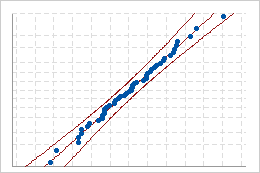
Ajuste adecuado
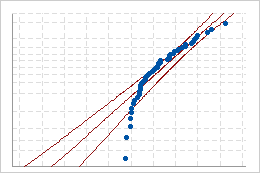
Ajuste deficiente
Nota
Si los datos originales están normalmente distribuidos, Minitab muestra solo una gráfica de probabilidad individual y no realiza la transformación de Johnson.
N
El número de valores presentes en la muestra. N es el conteo de todos los valores observados.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretación
Utilice N para evaluar el tamaño de la muestra.
Important
Interprete los resultados de una muestra muy pequeña o muy grande con precaución. Si tiene una muestra muy pequeña, una prueba de bondad de ajuste pudiera no tener suficiente potencia para detectar alejamientos significativos de la distribución. Si tiene una muestra muy grande, la prueba pudiera tener tanta potencia que detecte alejamientos incluso pequeños de la distribución que no tengan significancia práctica. Utilice las gráficas de probabilidad, además de los valores p, para evaluar el ajuste de distribución.
AD
El estadístico de bondad de ajuste de Anderson-Darling (AD) es una medida de las desviaciones entre la línea ajustada (con base en la distribución seleccionada) y la función de paso no paramétrica (con base en los puntos de datos). El estadístico de Anderson-Darling es una distancia elevada al cuadrado que tiene mayor ponderación en las colas de la distribución.
Interpretación
Minitab utiliza el estadístico de Anderson-Darling para calcular el valor p. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula de que los datos siguen la distribución.
Generalmente, valores substancialmente menores del estadístico de Anderson-Darling indican que los datos siguen una distribución más de cerca. Sin embargo, evite comparar directamente los valores AD en diferentes distribuciones cuando los valores AD son cercanos, porque los estadísticos AD se distribuyen de manera diferente para distintas distribuciones. Para comparar mejor el ajuste de diferentes distribuciones, utilice criterios adicionales, tales como las gráficas de probabilidades, los valores p y su conocimiento del proceso.
Valor p
Para los valores de datos originales y transformados, Minitab indica un valor p para la prueba de normalidad de Anderson-Darling (AD). El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Para una prueba de normalidad AD, la hipótesis nula es que los datos siguen la distribución normal. Por lo tanto, valores p más pequeños proporcionan evidencia más fuerte de que los datos no siguen la distribución normal.
Interpretación
Utilice el valor p para evaluar si los datos originales y transformados siguen la distribución normal. Generalmente, un valor p más grande indica un mejor ajuste de los datos.
- Un valor p que es menor que alfa indica que la distribución normal no provee un ajuste adecuado.
- Un valor p que es mayor que o igual a alfa indica que no hay suficiente evidencia de un ajuste de distribución deficiente. Usted puede presuponer que los datos siguen la distribución normal.
Si la transformación de Johnson es efectiva, el valor p de los datos transformados es mayor que alfa.
Important
Interprete los resultados de una muestra muy pequeña o muy grande con precaución. Si tiene una muestra muy pequeña, una prueba de bondad de ajuste pudiera no tener suficiente potencia para detectar alejamientos significativos de la distribución. Si tiene una muestra muy grande, la prueba pudiera tener tanta potencia que detecte alejamientos incluso pequeños de la distribución que no tengan significancia práctica. Utilice las gráficas de probabilidad, además de los valores p, para evaluar el ajuste de distribución.
Seleccionar una gráfica de transformación
La gráfica Seleccionar una transformación grafica el valor p calculado de la prueba de normalidad AD de cada valor Z para diferentes funciones de la transformación de Johnson. Para encontrar el valor Z óptimo, la transformación de Johnson utiliza una cuadrícula de valores Z sobre un rango de 0.25 a 1.25 con un incremento de 0.01 para una amplia gama de distribuciones. Minitab calcula el valor p de los datos transformados para cada valor Z y selecciona la función de transformación que tenga el valor p más grande que sea mayor que el criterio del valor p especificado para el análisis.
Interpretación
Utilice la gráfica Seleccionar una transformación para visualizar cómo la función de la transformación de Johnson se selecciona para producir el mejor ajuste para los datos. La línea de referencia horizontal muestra el criterio para el valor p especificado para el análisis. La línea de referencia vertical muestra el valor Z de la transformación que produce el mejor ajuste. Este valor Z máximo corresponde al valor p mínimo de la prueba de normalidad AD.
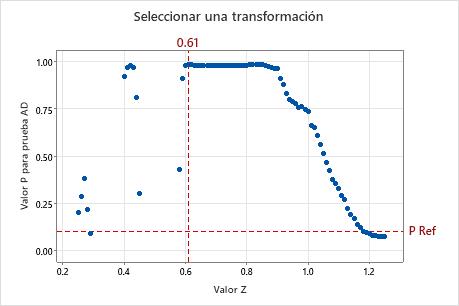
Nota
La tabla debajo de la gráfica (no se muestra aquí) muestra las estimaciones de parámetros de la mejor función de transformación. Para obtener más información sobre el algoritmo que utiliza Minitab para definir la función de transformación de Johnson, vaya a Métodos y fórmulas para las transformaciones en Identificación de distribución individual y haga clic en "Métodos y fórmulas para la transformación de Johnson".
Valor p para mejor ajuste
El valor p para mejor ajuste indica el valor p para la función de transformación de Johnson que produce el mejor ajuste de los datos transformados para seguir la distribución normal. Este valor p, redondeado al milésimo más cercano, también se muestra en la gráfica de probabilidad de los datos transformados.
Para obtener más información sobre cómo interpretar el valor p, véase la sección sobre el valor p.
Para obtener más información sobre cómo Minitab selecciona la función de transformación de Johnson con el mejor ajuste, véase la sección sobre la gráfica Seleccionar una transformación.
Z para mejor ajuste
El valor Z para mejor ajuste indica el valor Z para la función de transformación de Johnson que produce el mejor ajuste de los datos transformados para seguir la distribución normal. El valor Z óptimo se corresponde con el valor p para el mejor ajuste, como se muestra en la gráfica de la mejor transformación.
Para obtener más información sobre cómo Minitab utiliza el valor Z para seleccionar la función de transformación de Johnson con el mejor ajuste, véase la sección sobre la gráfica Seleccionar una transformación.
Mejor tipo de transformación
La transformación de Johnson selecciona de manera óptima una de las tres familias de distribución: SB, SL y SU, donde B, L y U se refieren a que la variable es una variable limitada, lognormal e ilimitada, respectivamente. Minitab utiliza la función de distribución seleccionada para transformar los datos de modo que sigan una distribución normal.
Para obtener más información sobre el algoritmo que utiliza Minitab para definir la función de transformación de Johnson, vaya a Métodos y fórmulas para las transformaciones en Identificación de distribución individual y haga clic en "Métodos y fórmulas para la transformación de Johnson".
Función de transformación de Johnson
Minitab muestra los parámetros de la función de transformación de Johnson que produce el mejor ajuste. Minitab utiliza esta función para transformar los datos originales.
Por ejemplo, supongamos que la función de transformación de Johnson es 0.762475 + 0.870902 × Ln(( X – 46.3174)/(59.6770 – X)). Si el valor de los datos originales de X es 50, entonces el valor de los datos transformados de 50 se calcula como 0.762475 + 0.870902 × Ln((50 – 46.3174)/(59.677 – 50)), que es igual a –0.07893.
Nota
Para almacenar todos los valores transformados en la hoja de trabajo, ingrese una columna de almacenamiento cuando realice el análisis.
Para obtener más información sobre el algoritmo que utiliza Minitab para definir la función de transformación de Johnson, vaya a Métodos y fórmulas para las transformaciones en Identificación de distribución individual y haga clic en "Métodos y fórmulas para la transformación de Johnson".
