Transformación de Box-Cox
La transformación de Box-Cox estima un valor de lambda, como se muestra en la siguiente tabla, que minimiza la desviación estándar de una variable transformada estandarizada. La transformación resultante es Yλ cuando λ ҂ 0 y ln Y cuando λ = 0.
El método de Box-Cox busca entre muchos tipos de transformaciones. La siguiente tabla muestra algunas transformaciones comunes donde Y' es la transformación de los datos Y.
| Valor de lambda (λ) | Transformación |
|---|---|
 |
 |
 |
 |
 |
 |
 |
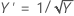 |
 |
 |
Algoritmo para la transformación de Johnson
La transformación de Johnson selecciona de manera óptima una de las tres familias de distribución para transformar los datos a fin de que sigan una distribución normal.
| Familia de Johnson | Función de transformación | Rango |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , donde
Senh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
El algoritmo utiliza el siguiente procedimiento:
- Considera casi todas las funciones de transformación potencial del sistema de Johnson.
- Estima los parámetros en la función utilizando el método descrito en Chou, et al.1
- Transforma los datos utilizando la función de transformación.
- Calcula los estadísticos de Anderson-Darling y el valor p correspondiente para los datos transformados.
- Selecciona la función de transformación que tiene el valor p más grande que sea mayor que el criterio del valor p (el valor predeterminado es 0.10) que usted especifique en el cuadro de diálogo Transformar. De lo contrario, no es apropiado una transformación.
Notación
| Término | Description |
|---|---|
| SB | La distribución de la familia de Johnson con la variable limitada (B) |
| SL | La distribución de la familia de Johnson con la variable lognormal (L) |
| SU | La distribución de la familia de Johnson con la variable ilimitada (U) |
Para obtener más información sobre la transformación de Johnson, véase Chou, et al.1 Minitab reemplaza la prueba de normalidad de Shapiro-Wilks utilizada en ese texto con la prueba de Anderson-Darling.
Para obtener información sobre la grásfica de probabilidad, percentiles y sus intervalos de confianza, vaya a Métodos y fórmulas para las distribuciones en Identificación de distribución individual.
