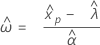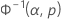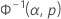En este tema
Gráfica de probabilidad
Las gráficas de probabilidad incluyen:
- Puntos, que son los percentiles estimados para las probabilidades correspondientes de un conjunto de datos ordenados.
- Líneas centrales, que representan el percentil esperado de la distribución basado en las estimaciones de los parámetros de máxima verosimilitud. Si la distribución provee un ajuste adecuado para los datos, los puntos se encuentran a lo largo de la línea del medio.
Probabilidades estimadas
Minitab estima la probabilidad (P) que se utiliza para calcular los puntos de la gráfica usando los siguientes métodos.
- Rango de medianas (método de Benard)
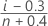
- Rango de medias (estimación de Herd-Johnson)
- Kaplan-Meier modificado (Hazen)
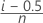
- Estimación de Kaplan-Meier de límite de producto
Notación
| Término | Description |
|---|---|
| n | Número de observaciones |
| i | Rango de la iésima observación observada x(i), donde x(1), x(2),...x(n) son los estadísticos ordenados o los datos ordenados del más pequeño al más grande |
Puntos de la gráfica
La línea intermedia de la gráfica de probabilidad se construye utilizando los cálculos de las coordenadas X y Y en esta tabla.
| Distribución | coordenada x | coordenada y |
|---|---|---|
| Valor extremo más pequeño | x | ln(–ln(1 – p)) |
| Valor extremo más grande | x | ln(–ln p) |
| Weibull | ln(x) | ln(–ln(1 – p)) |
| Weibull de 3 parámetros | ln(x – valor umbral) | ln(–ln(1 – p)) |
| Exponencial | ln(x) | ln(–ln(1 – p)) |
| Exponencial de 2 parámetros | ln(x – valor umbral) | ln(–ln(1 – p)) |
| Normal | x | Φ–1norm |
| Lognormal | ln(x) | Φ–1norm |
| Lognormal de 3 parámetros | ln(x – valor umbral) | Φ–1norm |
| Logística | x |
 |
| Loglogística | ln(x) |
 |
| Loglogística de 3 parámetros | ln(x – valor umbral) |
 |
| Gamma | x | Φ–1gamma |
| Gamma de 3 parámetros | ln(x – valor umbral) | Φ–1gamma |
Nota
Debido a que los puntos de la gráfica no dependen de ninguna distribución, son los mismos (antes de ser transformados) para cualquier gráfica de probabilidad. Sin embargo, la línea ajustada difiere dependiendo de la distribución paramétrica que se haya elegido.
Notación
| Término | Description |
|---|---|
| p | La probabilidad estimada |
| Φ-1norm | Valor devuelto para p por la CDF inversa para la distribución normal estándar |
| Φ-1gamma | Valor devuelto para p por la CDF inversa para la distribución gamma incompleta |
| ln(x) | El logaritmo natural de x |
Percentiles y error est. de percentiles
Un percentil es un valor en una escala de 100 que indica el porcentaje de una distribución que es igual o está por debajo de ese valor. Por opción predeterminada, Minitab muestra tablas de percentiles para análisis de distribuciones paramétricas de percentiles comunes.
Los errores estándar de las estimaciones de percentiles son la raíz cuadrada de las varianzas.
, 
, 
, 
, 
, 
, 
, 
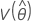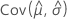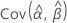y 
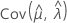denota las varianzas y covarianzas de las MLE de μ, σ, α, β, λ y θ tomadas del elemento adecuado de la inversa de la matriz de información de Fisher.
Las fórmulas utilizadas para estimaciones de percentiles y varianzas son las siguientes:
Distribución de valor extremo más pequeño
- Percentil
-
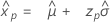
- Varianza
-
Distribución de valor extremo más grande
- Percentil
-
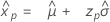
- Varianza
-
Distribución de Weibull
- Percentil
-
- Varianza
-
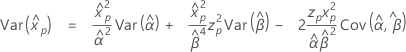
Distribución de Weibull de 3 parámetros
- Percentil
-
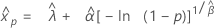
- Varianza
-
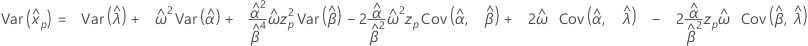
Distribución exponencial
- Percentil
-
- Varianza
-
Distribución exponencial de 2 parámetros
- Percentil
-
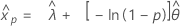
- Varianza
-
Distribución normal
- Percentil
-
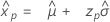
- Varianza
-
Distribución lognormal
- Percentil
-
- Varianza
-
Distribución lognormal de 3 parámetros
- Percentil
-
- Varianza
-
Distribución logística
- Percentil
-
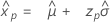
- Varianza
-
Distribución loglogística
- Percentil
-
- Varianza
-
Distribución loglogística de 3 parámetros
- Percentil
-
- Varianza
-
Distribución gamma
- Percentil
-
- Varianza
-
-
donde
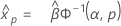
es la inversa de la distribución gamma incompleta regularizada
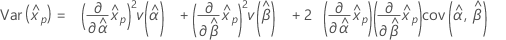
Distribución gamma de 3 parámetros
- Percentil
-
- Varianza
-
-
donde
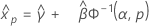
es la inversa de la distribución gamma incompleta regularizada
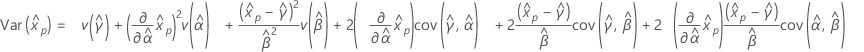
Límites de confianza para percentiles
| Distribución | Límites de confianza |
|---|---|
| Valor extremo más pequeño |
 |
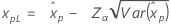| Valor extremo más grande |
 |
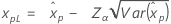| Normal |
 |
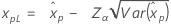| Logística |
 |
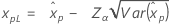| Weibull |
 |
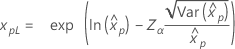| Exponencial |
 |
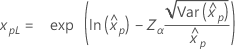| Lognormal |
 |
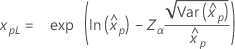| Loglogística |
 |
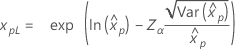| Weibull de 3 parámetros |
Si λ < 0:
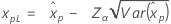 Si λ ≥ 0:
  |
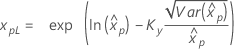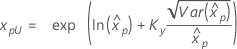| Exponencial de 2 parámetros |
Si λ < 0:
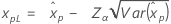 Si λ ≥ 0:
  |
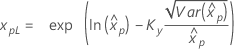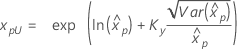| Lognormal de 3 parámetros |
Si λ < 0:
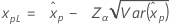 Si λ ≥ 0:
  |
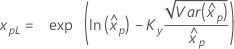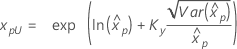| Loglogística de 3 parámetros |
Si λ < 0:
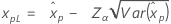 Si λ ≥ 0:
  |
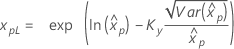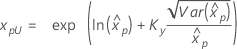Notación
| Término | Description |
|---|---|
| Kγ | El percentil (1 + γ) / 2 de una distribución normal estándar |
