Estimaciones máxima verosimilitud de los parámetros de distribución
El método de máxima verosimilitud se utiliza para estimar los valores de los parámetros de distribución que maximizan la función de verosimilitud de cada distribución. La meta es obtener la mejor "concordancia" entre el modelo de distribución y los datos de la muestra observados.
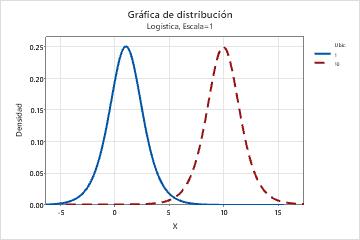
- Ubicación
- Este parámetro afecta la ubicación de una distribución. Por ejemplo, con
parámetros de ubicación diferentes, una distribución logística se puede
desplazar a lo largo del eje horizontal.
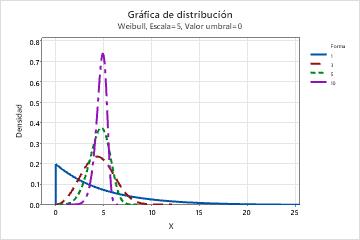
- Forma
- Este parámetro afecta la forma de la distribución. Por ejemplo, con
diferentes parámetros de forma, una distribución de Weibull puede parecer
más asimétrica o más simétrica.
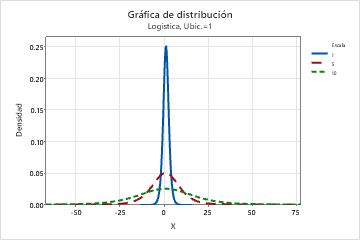
- Escala
- El parámetro de ubicación afecta la ubicación de una distribución. Por
ejemplo, con diferentes parámetros de escala, una distribución logística
puede parecer más "estirada" o más comprimida.
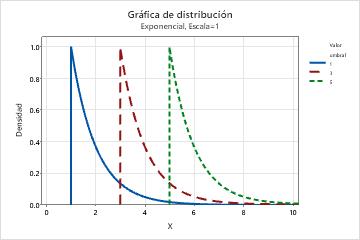
- Valor umbral
- Este parámetro afecta el valor mínimo de una variable aleatoria. Por
ejemplo, con diferentes parámetros umbral, una distribución exponencial se
puede definir en un rango diferente de valores.
Nota
Minitab calcula las estimaciones de parámetros utilizando el método de máxima verosimilitud para todas las distribuciones, excepto las distribuciones normal y lognormal, que en su lugar usan estimaciones de parámetros sin sesgo.
Interpretación
Utilice las estimaciones de máxima verosimilitud de los parámetros de distribución para entender el modelo de distribución específico que se usa en sus datos. Por ejemplo, supongamos que un ingeniero especializado en calidad decide que, con base en el conocimiento histórico del proceso y los valores de Anderson-Darling y p para LRT, la distribución Weibull de 3 parámetros proporciona el mejor ajuste para los datos del proceso. Para entender la distribución de Weibull de 3 parámetros específica que se utiliza para modelar los datos, el ingeniero examina las estimaciones de máxima verosimilitud de forma, escala y valor umbral que se calculan para la distribución.
Distribución
La identificación de distribución individual proporciona estadísticos de bondad de ajuste y parámetros de distribución para varias distribuciones comúnmente utilizadas. Muchas de estas distribuciones son versátiles y pueden modelar una variedad de datos continuos, incluidos datos con valores positivos, valores negativos y 0.
- Lognormal de 2 parámetros
- Exponencial de 1 parámetro
- Weibull de 2 parámetros
- Gamma de 2 parámetros
- Loglogística de 2 parámetros
Por lo tanto, si sus datos contienen valores negativos o 0, Minitab no indica los resultados para estas distribuciones específicas. En ese caso, utilice los resultados de la versión de parámetro más alto de cada distribución. Por ejemplo, si sus datos contienen valores negativos, Minitab no indica los resultados de la distribución lognormal de 2 parámetros. En su lugar, utilice la distribución lognormal de 3 parámetros.
Para obtener más información sobre las distribuciones utilizadas en identificación de distribución individual, vaya a ¿Por qué es Weibull la distribución predeterminada para el análisis de capacidad no normal?.
Nota
Para obtener información sobre las fórmulas que se utilizan para calcular la PDF y la CDF de cada distribución, vaya a Métodos y fórmulas para las distribuciones en Identificación de distribución individual.
