N
El número de valores presentes en la muestra. N es el conteo de todos los valores observados.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretación
Utilice N para evaluar el tamaño de la muestra.
Important
Interprete los resultados de una muestra muy pequeña o muy grande con precaución. Si tiene una muestra muy pequeña, una prueba de bondad de ajuste pudiera no tener suficiente potencia para detectar alejamientos significativos de la distribución. Si tiene una muestra muy grande, la prueba pudiera tener tanta potencia que detecte alejamientos incluso pequeños de la distribución que no tengan significancia práctica. Utilice las gráficas de probabilidad, además de los valores p, para evaluar el ajuste de distribución.
N*
El número de valores faltantes en la muestra. N* es el conteo de las celdas en la hoja de trabajo que contienen el símbolo de valor faltante *.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Media
La media se calcula como el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
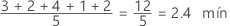
Interpretación
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como un punto de referencia estándar.
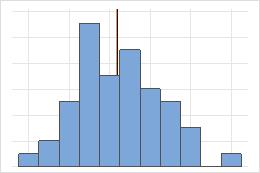
Media y mediana en una distribución simétrica
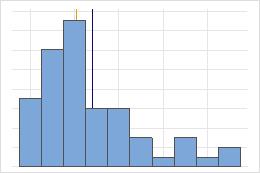
Media y mediana en una distribución no simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son casi iguales. Por lo tanto, las líneas se sobreponen y no se pueden distinguir entre sí. En la distribución no simétrica, los datos son asimétricos a la derecha, lo que causa que el valor de la media sea mayor que la mediana.
Desv.Est.
La desviación estándar (Desv.Est.) es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población y s se utiliza para representar la desviación estándar de una muestra.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Una mayor desviación estándar de la muestra indica que los datos están dispersos más ampliamente alrededor de la media.
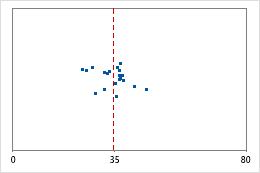
Hospital 1
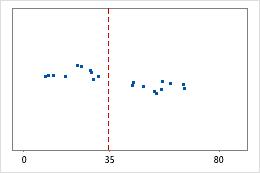
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Mediana
La mediana es el punto medio del conjunto de datos. El valor de este punto medio es el punto en el cual la mitad de las observaciones está por encima del valor y la otra mitad está por debajo del valor. La mediana se determina jerarquizando las observaciones y hallando la observación que ocupe el número [N + 1] / 2 en el orden jerarquizado. Si el número de observaciones es par, la mediana es el valor entre las observaciones jerarquizadas en los números N / 2 y [N / 2] + 1.
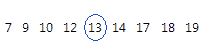
Para estos datos ordenados, la mediana es 13. Es decir, la mitad de los valores es menor que o igual a 13 y la otra mitad de los valores es mayor que o igual a 13.
Interpretación

Media y mediana en una distribución simétrica

Media y mediana en una distribución no simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son casi iguales. Por lo tanto, las líneas se sobreponen y no se pueden distinguir entre sí. En la distribución no simétrica, los datos son asimétricos a la derecha, lo que causa que el valor de la media sea mayor que la mediana.
Mínimo
El valor de datos más pequeño.
En estos datos, el mínimo es 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el mínimo para identificar un posible valor atípico. Si el valor es extrañamente bajo, investigue las posibles causas, como un error de ingreso de datos o un error de medición.
Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo para determinar su rango. El rango es la diferencia entre el valor máximo y el mínimo en el conjunto de datos. Cuando usted evalúa la dispersión de los datos, también considere otras medidas, como la desviación estándar.
Máximo
El valor de datos más grande.
En estos datos, el máximo es 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el máximo para identificar un posible valor atípico. Si el valor es extrañamente alto, investigue las posibles causas, como un error de ingreso de datos o un error de medición.
Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo para determinar su rango. El rango es la diferencia entre el máximo y el mínimo en el conjunto de datos. Cuando usted evalúa la dispersión de los datos, también considere otras medidas, como la desviación estándar.
Asimetría
La asimetría es el grado en que los datos no son simétricos.
Interpretación
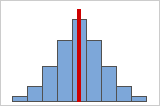
Figura A: Datos simétricos distribuidos normalmente
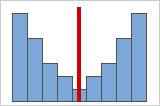
Figura B: Datos simétricos no distribuidos normalmente
Distribuciones simétricas o no asimétricas
A medida que los datos son más simétricos, su valor de asimetría se acerca a 0. La Figura A muestra datos distribuidos normalmente, que por definición presentan relativamente poca asimetría. La línea en la mitad de este histograma de datos normales muestra que un lado es el reflejo del otro. Sin embargo, la ausencia de asimetría por sí sola no implica normalidad. La Figura B muestra una distribución en la que ambos lados son un reflejo el uno del otro, pero los datos no están distribuidos normalmente.
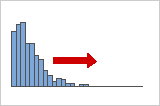
Distribuciones asimétricas positivas o hacia la derecha
Los datos asimétricos positivos también se denominan datos asimétricos hacia la derecha porque la "cola" de la distribución apunta hacia la derecha. Los datos asimétricos positivos tienen un valor de asimetría que es mayor que 0. Los datos de salario a menudo tienen asimetría positiva: muchos empleados en una compañía tienen salarios relativamente bajos, mientras que cada vez menos gente devenga salarios muy altos.
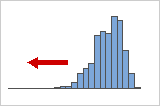
Distribuciones asimétricas negativas o hacia la izquierda
Los datos asimétricos negativos a menudo se llaman datos asimétricos hacia la izquierda porque la "cola" de la distribución apunta hacia la izquierda. Los datos asimétricos negativos tienen un valor de asimetría que es menor que 0. Los datos sobre tasa de fallas a menudo son asimétricos negativos. Por ejemplo, muy pocas bombillas se queman inmediatamente y la mayoría no se queman sino hasta después de un largo tiempo.
Curtosis
La curtosis indica la manera en que las colas de una distribución difieren de la distribución normal.
Interpretación
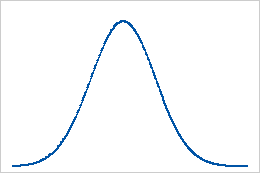
Línea de base: Valor de curtosis de 0
Los datos que siguen una distribución normal perfectamente tienen un valor de curtosis de 0. Los datos distribuidos normalmente establecen la línea de base para la curtosis. Una curtosis que se desvía significativamente de 0 puede indicar que los datos no están distribuidos normalmente.
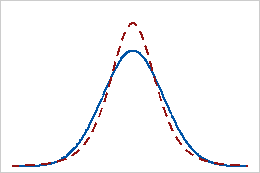
Curtosis positiva
Una distribución que tiene un valor positivo de curtosis indica que la distribución tiene colas más pesadas que la distribución normal. Por ejemplo, los datos que siguen una distribución t tienen un valor positivo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución t con un valor positivo de curtosis.
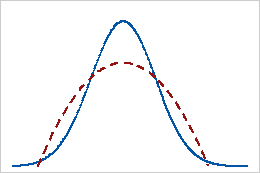
Curtosis negativa
Una distribución que tiene un valor negativo de curtosis indica que la distribución tiene colas más livianas que la distribución normal. Por ejemplo, los datos que siguen una distribución beta con el primer y el segundo parámetro de forma iguales a 2 tienen un valor negativo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución beta con curtosis negativa.
