Ejemplo de Identificación de distribución individual

Un ingeniero especializado en calidad que trabaja para una empresa de suplementos nutricionales desea evaluar el contenido de calcio en las cápsulas de vitamina. El ingeniero toma una muestra aleatoria de cápsulas y registra su contenido de calcio. Para determinar cuál análisis estadístico es adecuado para los datos, el ingeniero primero debe determinar la distribución de datos.

El ingeniero realiza la identificación de distribución individual para determinar qué distribución se ajusta mejor a los datos.

Abra los datos de muestra, ContenidoCalcio.MTW.
Elija Estadísticas > Herramientas de calidad > Identificación de distribución individual.
En Los datos están organizados como, seleccione Columna individual y luego ingrese Calcio.
En Tamaño del subgrupo, ingrese 1.
Haga clic en Aceptar.

Interpretar los resultados

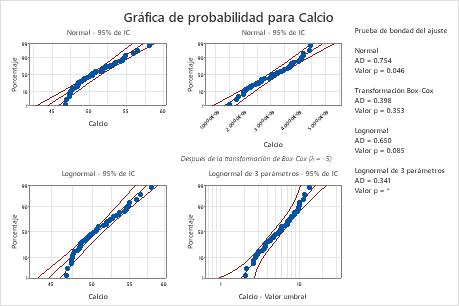
Minitab muestra una gráfica de probabilidad y el valor p de cada distribución y transformación. Si una distribución provee un buen ajuste para los datos (o si una transformación es efectiva), los puntos en la gráfica siguen una línea recta dentro de los bordes de confianza y el valor p es mayor que el nivel de significancia. A menudo se utiliza un nivel de significancia de 0.05. El valor p para la prueba de relación de verosimilitud (LRT) indica si agregar un parámetro adicional a una distribución mejora significativamente su ajuste. Un valor p para LRT menor que 0.05 sugiere que la mejora es significativa.

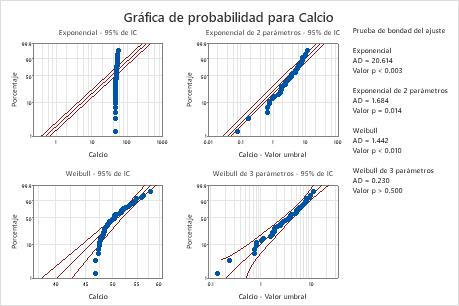
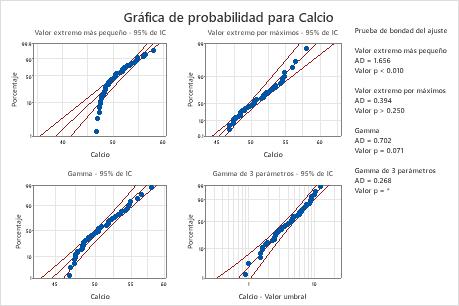
Para estos datos, la distribución de Weibull de 3 parámetros (p > 0.500) y la distribución de valor extremo más grande (p > 0.250) proporcionan un ajuste adecuado para los datos. Agregar un tercer parámetro mejora significativamente el ajuste de la distribución lognormal (LRT P = 0.017), la distribución de Weibull (LRT P = 0.000), la distribución gamma (LRT P = 0.006) y la distribución loglogística (LRT P = 0.027).

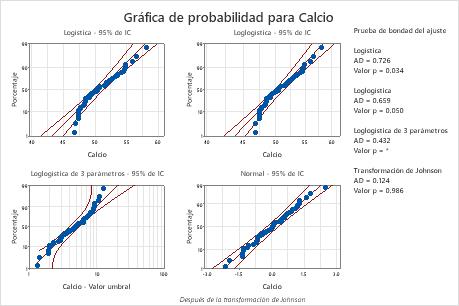
La transformación de Box-Cox (p = 0.324) y la transformación de Johnson (p = 0.986) son efectivas para estos datos. Después de la transformación, la distribución normal proporciona un ajuste adecuado para los valores transformados.

Exponencial de 2 parámetros

* ADVERTENCIA * La matriz de varianzas y covarianzas de los parámetros estimados no existe.
Se supone que el parámetro de valor umbral es fijo cuando se calculan intervalos de
confianza.

Gamma de 3 parámetros

* ADVERTENCIA * La matriz de varianzas y covarianzas de los parámetros estimados no existe.
Se supone que el parámetro de valor umbral es fijo cuando se calculan intervalos de
confianza.

Distribución	AD	P	LRT P
Normal	0.754	0.046
Transformación Box-Cox	0.414	0.324
Lognormal	0.650	0.085
Lognormal de 3 parámetros	0.341	*	0.017
Exponencial	20.614	<0.003
Exponencial de 2 parámetros	1.684	0.014	0.000
Weibull	1.442	<0.010
Weibull de 3 parámetros	0.230	>0.500	0.000
Valor extremo más pequeño	1.656	<0.010
Valor extremo por máximos	0.394	>0.250
Gamma	0.702	0.071
Gamma de 3 parámetros	0.268	*	0.006
Logística	0.726	0.034
Loglogística	0.659	0.050
Loglogística de 3 parámetros	0.432	*	0.027
Transformación de Johnson	0.124	0.986

Distribución	Ubicación	Forma	Escala	Valor umbral
Normal*	50.78200		2.76477
Transformación de Box-Cox*	0.00000		0.00000
Lognormal*	3.92612		0.05368
Lognormal de 3 parámetros	1.69295		0.46849	44.74011
Exponencial			50.78200
Exponencial de 2 parámetros			4.06326	46.71873
Weibull		17.82470	52.13681
Weibull de 3 parámetros		1.47605	4.53647	46.66579
Valor extremo más pequeño	52.22257		2.95894
Valor extremo por máximos	49.50370		2.16992
Gamma		351.04421	0.14466
Gamma de 3 parámetros		2.99218	1.63698	45.88376
Logística	50.57182		1.59483
Loglogística	3.92259		0.03121
Loglogística de 3 parámetros	1.54860		0.32763	45.46180
Transformación de Johnson*	0.02897		0.97293

Ejemplo de Identificación de distribución individual

Interpretar los resultados

Exponencial de 2 parámetros

Gamma de 3 parámetros

Estadísticas descriptivas

Prueba de bondad del ajuste

Estimaciones ML de los parámetros de distribución