¿Qué es el %tolerancia?
Un estadístico que es afectado directamente por los límites de especificación es el estadístico %tolerancia, el cual compara la tolerancia con la variación del estudio. La situación ideal es que la tolerancia englobe ampliamente la variación del estudio, garantizando que la variabilidad producida por el R&R del sistema de medición y la variación entre las partes no lleven la salida del proceso más allá de los límites de especificación.
Cuando un proceso tiene dos límites de especificación, la tolerancia es igual a la diferencia entre ellos y el %Tolerancia es igual a la variación del estudio de una fuente de variación dada dividida entre esta tolerancia. Sin embargo, este método no es válido cuando usted indica un solo límite de especificación.
Ejemplo de procesos con un límite de especificación
Muchos procesos operan con un solo límite de especificación. Por ejemplo, un aserradero corta vigas de modo que estén perfectamente rectas, pero, frecuentemente, las vigas se tuercen durante la producción. Las mediciones de esta torcedura tienen un límite de especificación superior para distinguir entre grados de torcedura aceptables e inaceptables. Sin embargo, estas mediciones no tienen un límite de especificación inferior, porque no pueden tener valores menores que cero. De hecho, el cero representa una viga perfectamente recta, sin torcedura. Además, algunos procesos tienen un límite de especificación inferior, pero no un límite de especificación superior. Un fabricante de cubiertos debe verificar que la dureza de los filos de sus cuchillos sea mayor que 55 en la escala C de Rockwell. El límite de especificación inferior es 55, pero no existe ningún límite de especificación superior.
Cómo calcula Minitab el %tolerancia cuando ingreso una tolerancia unilateral
- Minitab calcula una variación unilateral del proceso dividiendo el estadístico de variación del estudio entre 2.
- Minitab define la tolerancia unilateral como el valor absoluto de la diferencia entre el único límite de especificación y el valor medio de todas las mediciones.
- Minitab calcula el estadístico %tolerancia dividiendo la variación unilateral del proceso entre la tolerancia unilateral.

| Término | Description |
|---|---|
| L | el único límite de especificación |
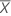 | la media de todas las observaciones |
Nota
Si la media de todas las observaciones es menor que el límite de especificación inferior, o mayor que el límite de especificación superior, las mediciones se desvían fuertemente de su rango aceptable y el %tolerancia no se calcula.
