En este tema
GL
Los grados de libertad (GL) para cada SC (suma de los cuadrados). En general, GL mide qué tanta información está disponible para calcular cada SC.
SC
La suma de los cuadrados (SC) es la suma de las distancias al cuadrado y representa una medida de la variabilidad que se debe a diferentes fuentes. SC total indica la cantidad de variabilidad en los datos a partir de la media general. SC operador indica la cantidad de variabilidad entre la medición promedio de cada operador y la media general.
SC Total = SC Operador + SC Parte (Operador) + SC Repetibilidad
CM
Los cuadrados medios (CM) son la variabilidad en los datos que se debe a diferentes fuentes. CM representa el hecho de que las diferentes fuentes tienen diferentes números de niveles o valores posibles.
CM = SC/GL para cada fuente de variabilidad
F
El estadístico que se utiliza para determinar si los efectos del Operador o la Parte (Operador) influyen de manera significativa en la medición.
Mientras más grande sea el estadístico F, más probabilidades hay de que el factor contribuya significativamente a la variabilidad en la respuesta o la variable de medición.
P
El valor p es la probabilidad de obtener un estadístico de prueba (como el estadístico F) que sea por lo menos tan extremo como el valor calculado a partir de la muestra, si la hipótesis nula es verdadera.
Interpretación
Utilice el valor p de la tabla ANOVA para determinar si las mediciones promedio son significativamente diferentes.
Un valor p bajo indica que el supuesto de que todos los operadores o partes (operadores) comparten la misma media probablemente no es cierto.
- Valor p ≤ α: Al menos una media es estadísticamente diferente
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula y concluye que al menos una de las medias es significativamente diferente de las demás. Por ejemplo, al menos uno de los operadores mide de manera diferente.
- Valor p > α: Las medias no son significativamente diferentes
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula, porque no cuenta con suficiente evidencia para concluir que las medias de la población son diferentes. Por ejemplo, no puede concluir que los operadores miden de manera diferente.
CompVar
CompVar es los componentes de la varianza estimada para cada fuente en una tabla ANOVA.
Interpretación
Utilice los componentes de la varianza para evaluar la variación para cada fuente del error de medición.
En un sistema de medición aceptable, el componente más grande de la variación es la variación entre las partes. Si la repetibilidad y la reproducibilidad contribuyen con grandes cantidades de variación, debe investigar el origen del problema y tomar medidas correctivas.
%Contribución (de CompVar)
%Contribución es el porcentaje de la variación total que corresponde a cada componente de la varianza. Se calcula como el componente de la varianza para cada fuente dividido entre la variación total y luego multiplicado por 100 para expresarlo como un porcentaje.
Interpretación
Utilice el %Contribución para evaluar la variación de cada fuente del error de medición.
En un sistema de medición aceptable, el componente más grande de la variación es la variación entre las partes. Si la repetibilidad y la reproducibilidad contribuyen con grandes cantidades de variación, debe investigar el origen del problema y tomar medidas correctivas.
Desv.Est. (DE)
Desv.Est. (DE) es la desviación estándar para cada fuente de variación. La desviación estándar es igual a la raíz cuadrada del componente de la varianza para esa fuente.
La desviación estándar es una medida conveniente de la variación, porque tiene las mismas unidades que las mediciones de las partes y la tolerancia.
Var. del estudio (6 * DE)
La variación del estudio se calcula como la desviación estándar para cada fuente de variación multiplicada por 6 o el multiplicador que usted especifique en Variación del estudio.
Por lo general, la variación del proceso se define como 6s, donde s es la desviación estándar como una estimación de la desviación estándar de la población (denotada por σ o sigma). Cuando los datos siguen una distribución normal, aproximadamente 99.73% de los datos están dentro de 6 desviaciones estándar con respecto a la media. Para definir un porcentaje diferente de datos, utilice otro multiplicador de la desviación estándar. Por ejemplo, si desea saber dónde se ubica el 99% de los datos, tendría que usar un multiplicador de 5.15, en vez del multiplicador predeterminado de 6.
%Var. del estudio (%VE)
El %Var. del estudio se calcula como la variación del estudio para cada fuente de variación, dividida entre la variación total y multiplicada por 100.
El %Var. del estudio es la raíz cuadrada del componente de la varianza (CompVar) para esa fuente. Por lo tanto, el %Contribución de los valores de CompVar suman 100, pero el %Var. del estuidio no.
Interpretación
Utilice %Var. del estudio para comparar la variación del sistema de medición con la variación total. Si utiliza el sistema de medición para evaluar las mejoras del proceso, como la reducción de la variación entre las partes, el %Var. del estudio es una mejor estimación de la precisión de las mediciones. Si desea determinar la capacidad del sistema de medición para evaluar las partes en comparación con la especificación, el %Tolerancia es la métrica adecuada.
%Tolerancia (VE/Toler)
El %Tolerancia se calcula como la variación del estudio para cada fuente dividida entre la tolerancia del proceso y luego multiplicada por 100.
Si usted ingresa la tolerancia, Minitab calcula el %Tolerancia, que compara la variación del sistema de medición con las especificaciones.
Interpretación
Utilice el %Ttolerancia para evaluar las partes en relación con las especificaciones. Si utiliza el sistema de medición para mejorar procesos, como la reducción de la variación entre las partes, el %Var. del estudio es la métrica adecuada.
%Proceso (VE/Proc)
Si usted ingresa una desviación estándar histórica, pero utiliza las partes incluidas en el estudio para estimar la variación del proceso, entonces Minitab calcula el %Proceso. El %Proceso compara la variación del sistema de medición con la variación histórica del proceso. El %Proceso se calcula como la variación del estudio para cada fuente, dividida entre la variación histórica del proceso y multiplicada por 100. Por opción predeterminada, la variación del proceso es igual a 6 veces la desviación estándar histórica.
Si usted utiliza una desviación estándar histórica para estimar la variación del proceso, entonces Minitab no muestra el %Proceso, porque el %Proceso es idéntico al %Var. del estudio.
IC 95%
Los intervalos de confianza de 95% (IC 95%) son los rangos de valores que es probable que contengan el valor real de cada métrica del error de medición.
Minitab proporciona intervalos de confianza para los componentes de la varianza, el % de contribución de los componentes de la varianza, la desviación estándar, la variación del estudio, el % de variación del estudio, el % de tolerancia y el número de categorías distintas.
Interpretación
Puesto que las muestras de datos son aleatorias, es poco probable que dos estudios del sistema de medición produzcan intervalos de confianza idénticos. Sin embargo, si usted repite los estudios muchas veces, un cierto porcentaje de los intervalos de confianza resultantes contendrá el error de medición real desconocido. El porcentaje de estos intervalos de confianza que contiene el parámetro es el nivel de confianza del intervalo.
Por ejemplo, con un nivel de confianza de 95%, usted puede estar 95% seguro de que el intervalo de confianza contiene el valor real. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen importancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
Supongamos que el CompVar para la repetibilidad es 0.044727 y el IC de 95% correspondiente es (0.035, 0.060). La estimación de la variación para la repetibilidad calculada a partir de los datos es 0.044727. Usted puede estar 95% seguro de que el intervalo de 0.035 a 0.060 contiene la variación real de la repetibilidad.
Número de categorías distintas
El número de categorías distintas es una métrica que se utiliza en los estudios R&R del sistema de medición para identificar la capacidad de un sistema de medición de detectar una diferencia en la característica medida. Este número representa la cantidad de intervalos de confianza no superpuestos que abarcan el rango de variación del producto, que es definido por las muestras seleccionadas. También puede entenderse como el número de grupos dentro de los datos del proceso que el sistema de medición puede discernir.
Interpretación
El manual de análisis de sistemas de medición 1 publicado por el Automobile Industry Action Group (AIAG) señala que 5 o más categorías indican un sistema de medición aceptable. Si el número de categorías distintas es menor que 5, es posible que el sistema de medición no tenga suficiente resolución.
Por lo general, cuando el número de categorías distintas es menor que 2, el sistema de medición no es útil para controlar el proceso, porque no puede distinguir entre las partes. Cuando el número de categorías distintas es 2, los datos solo pueden dividirse en dos grupos, como por ejemplo alto y bajo. Cuando el número de categorías distintas es 3, las partes pueden dividirse en 3 grupos, como bajo, medio y alto.
Para obtener más información, vaya a Uso del número de categorías distintas.
Probabilidades de clasificación errónea
Cuando se especifica por lo menos un límite de especificación, Minitab puede calcular las probabilidades de que se realice una clasificación errónea de un producto. Debido a la variación del sistema de medición, el valor medido de la parte no siempre es igual al valor real de la parte. La discrepancia entre el valor medido y el valor real crea el potencial para clasificar erróneamente la parte.
- Probabilidad conjunta
- Utilice la probabilidad conjunta cuando no tenga conocimiento previo sobre la aceptabilidad de las partes. Por ejemplo, usted toma una muestra de una línea de producción y no sabe si cada parte específica es una parte buena o mala. Hay dos tipos de clasificación errónea que pueden ocurrir:
- La probabilidad de que la parte esté mala y usted la acepte.
- La probabilidad de que la parte esté buena y usted la rechace.
- Probabilidad condicional
- Utilice la probabilidad condicional cuando tenga conocimiento previo sobre la aceptabilidad de las partes. Por ejemplo, usted toma una muestra de una pila de unidades reparadas o de una pila de productos que pronto se enviarán como partes buenas. Hay dos tipos de clasificación errónea que pueden ocurrir:
- La probabilidad de que usted acepte una parte seleccionada de una pila de productos malos que deben repararse (también conocida como falsa aceptación).
- La probabilidad de que usted rechace una parte seleccionada de una pila de productos buenos que están a punto de ser enviados (también conocida como falso rechazo).
Interpretación
Probabilidad conjunta
| Descripción | Probabilidad |
|---|---|
| Se aceptó una parte seleccionada aleatoriamente que está en mal estado | 0.037 |
| Se rechazó una parte seleccionada aleatoriamente que está en buen estado | 0.055 |
Probabilidad condicional
| Descripción | Probabilidad |
|---|---|
| Se aceptó una parte proveniente de un grupo de productos en mal estado | 0.151 |
| Se rechazó una parte proveniente de un grupo de productos en buen estado | 0.073 |
La probabilidad conjunta de que una parte esté mala y usted la acepte es de 0.037. La probabilidad conjunta de que una parte esté buena y usted la rechace es de 0.055.
La probabilidad condicional de una falsa aceptación, que usted acepte una parte durante la reinspección cuando realmente está fuera de las especificaciones, es de 0.151. La probabilidad condicional de un falso rechazo, que usted rechace una parte durante la reinspección cuando realmente está dentro de las especificaciones, es de 0.073.
VDA 5
Nota
VDA 5 está solo en la aplicación web.
Nota
El análisis utiliza la incertidumbre máxima entre uEVR, uRE y uEVO para calcular la variación del proceso de medición. Falta el % del total para las otras 2 estadísticas porque esas estadísticas no contribuyen al total.
- Calibración (uCAL)
- La calibración (uCAL) es la incertidumbre en las mediciones de la calibración del patrón de referencia. Esta estadística es una entrada para el análisis. Por lo general, este valor proviene del certificado de calibración.
- Repetibilidad en la referencia (uEVR)
- La repetibilidad en la referencia (uEVR) es la incertidumbre de las mediciones repetidas de la pieza de referencia por el mismo operador con el mismo dispositivo. Esta estadística es una entrada para el análisis. Por lo general, este valor proviene de un estudio tipo 1 del sistema de medición.
- Resolución (uRE)
- La resolución (uRE) es la incertidumbre debida a la resolución del medidor. El análisis calcula esta estadística cuando la resolución del medidor es una entrada para el análisis.
- Repetibilidad del objeto medido (uEVO)
- La repetibilidad del objeto medido (uEVO) es la incertidumbre debida a la repetibilidad en el estudio R&R del sistema de medición. La repetibilidad es la variabilidad en las mediciones cuando el mismo operador mide la misma pieza varias veces.
- Sesgo (uBI)
- El sesgo (uBI) es la incertidumbre en las mediciones debido a la diferencia entre la medición de referencia conocida y el promedio de las mediciones en el estudio. Esta estadística es una entrada para el análisis. Por lo general, este valor proviene de un estudio de sesgo donde la parte de referencia está dentro del rango de medidas.
- Linealidad (uLIN)
- La linealidad (uLIN) es la incertidumbre en las mediciones de la linealidad. La linealidad es la diferencia entre el valor de la pieza de referencia y la medida media que proviene del cambio en el sesgo a medida que cambia el valor de la pieza. Esta estadística es una entrada para el análisis. Por lo general, este valor proviene de un estudio de linealidad donde la parte de referencia estaba dentro del rango de medidas.
- Otros factores (uREST)
- Otros factores (uREST) es la incertidumbre en las mediciones debido a uno o más factores adicionales. Si las especificaciones para el análisis tienen un factor adicional, entonces esta incertidumbre es una entrada para el análisis. Si las especificaciones para el análisis tienen más de un factor, entonces esta incertidumbre combina los valores. Por ejemplo, utilice las especificaciones de otros factores para tener en cuenta la incertidumbre debida a la temperatura si las mediciones tienen diferencias más amplias cuando la recopilación de datos se realiza a una temperatura más alta.
- Operadores (uAV)
- Operadores (uAV) es la incertidumbre en las mediciones debido a la reproducibilidad en el estudio R&R del sistema de medición. La reproducibilidad es la variabilidad en las mediciones cuando diferentes operadores miden la misma pieza.
- Proceso de medición (uMP)
- El proceso de medición (uMP) combina todos los componentes de incertidumbre para estimar la incertidumbre total del proceso de medición.
- % del total
- Para cada fuente de incertidumbre, el análisis presenta el porcentaje del uMP que resulta de esa fuente. Utilice el porcentaje para comparar la cantidad de incertidumbre de las diferentes fuentes.
- % de tolerancia (%QMP)
- % de tolerancia (%QMP) combina la incertidumbre del proceso de medición con la variación del estudio y compara el valor con la tolerancia del proceso. %QMP es una forma común de decidir si un proceso de medición es satisfactorio. En algunas aplicaciones, un valor del 30% o menos indica que un proceso de medición es satisfactorio.
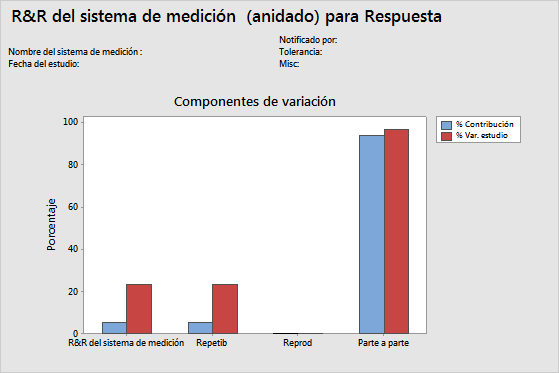
Gráfica Componentes de la variación
La gráfica Componentes de la variación es un resumen gráfico de los resultados de un estudio R&R del sistema de medición.
- R&R total del sistema de medición: La suma de los componentes de la varianza de repetibilidad y reproducibilidad.
- Repetibilidad: La variabilidad en las mediciones cuando el mismo operador mide partes del mismo lote.
- Reproducibilidad: La variabilidad en las mediciones cuando diferentes operadores miden las partes.
- Entre las partes: La variabilidad en las mediciones causada por las diferencias entre las partes.
Interpretación
- %Contribución
- %Contribución es el porcentaje de la variación total que corresponde a cada componente de la varianza. Se calcula como el componente de la varianza para cada fuente dividido entre la variación total y luego multiplicado por 100.
- %Var. del estudio
- %Var. del estudio es el porcentaje de la variación del estudio correspondiente a cada fuente. Se calcula como la variación del estudio para cada fuente dividida entre la variación total del estudio y luego multiplicada por 100.
- %Tolerancia
- El %Tolerancia compara la variación del sistema de medición con las especificaciones. Se calcula como la variación del estudio para cada fuente dividida entre la tolerancia del proceso y luego multiplicada por 100.
- %Proceso
- El %Proceso compara la variación del sistema de medición con la variación total. Se calcula como la variación del estudio para cada fuente dividida entre la variación histórica del proceso y luego multiplicada por 100.
En un sistema de medición aceptable, el componente más grande de la variación es la variación entre las partes.
Gráfica R
La gráfica R es una gráfica de control de rangos que muestra la consistencia de los operadores.
- Puntos graficados
- Para cada operador, la diferencia entre las mediciones máxima y mínima de cada parte. La gráfica R representa los puntos por operador para que se pueda observar qué tan consistente es cada operador.
- Línea central (Rbarra)
- El promedio general del proceso (es decir, el promedio de todos los rangos de muestras).
- Límites de control (LCI y LCS)
- La cantidad de variación que usted puede esperar para los rangos de las muestras. Para calcular los límites de control, Minitab utiliza la variación de cada muestra.
Nota
Si cada operador mide cada parte 9 veces o más, Minitab muestra una gráfica S en lugar de una gráfica R.
Interpretación
Un rango promedio pequeño indica que el sistema de medición tiene poca variación. Un punto mayor que el límite de control superior (LCS) indica que el operador no mide las partes consistentemente. El cálculo del LCS incluye el número de mediciones por parte que realiza un operador y la variación entre las partes. Si los operadores miden las partes consistentemente, entonces el rango entre las mediciones máxima y mínima es pequeña, en relación con la variación del estudio, y los puntos deberían estar bajo control.
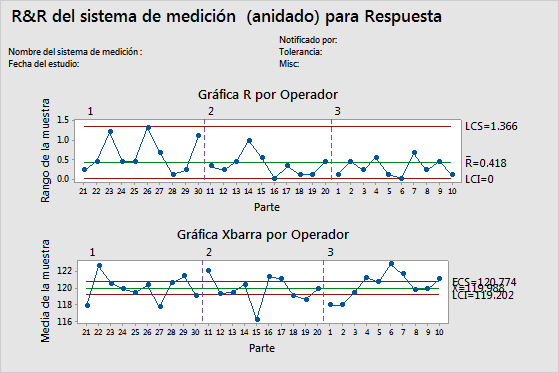
Gráfica Xbarra
La gráfica Xbarra compara la variación entre las partes con el componente de repetibilidad.
- Puntos graficados
- La medición promedio de cada parte, graficada para cada operador.
- Línea central (Xbarra)
- El promedio general para todas las mediciones de las partes realizadas por todos los operadores.
- Límites de control (LCI y LCS)
- Los límites de control se basan en la estimación de la repetibilidad y el número de mediciones en cada promedio.
Interpretación
Las partes que se seleccionan para un estudio R&R del sistema de medición deben representar todo el rango de partes posibles. Por lo tanto, esta gráfica debería indicar más variación entre los promedios de las partes que la que se podría esperar de la variación de la repetibilidad por sí sola.
En un escenario ideal, la gráfica tiene límites de control estrechos con muchos puntos fuera de control que indican un sistema de medición con poca variación.

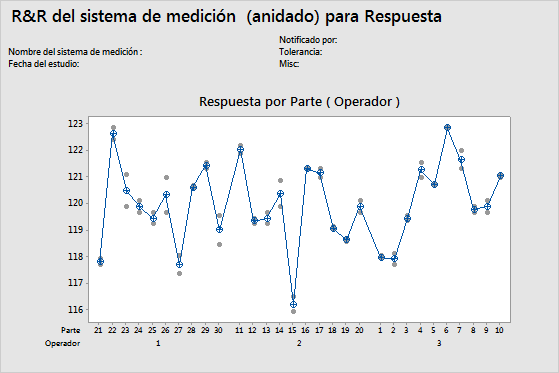
Gráfica Por parte (Operador)
La gráfica Por parte (Operador) muestra todas las mediciones que se tomaron en el estudio, organizadas por parte. Esta gráfica muestra las diferencias entre los niveles de los factores. Los estudios R&R del sistema de medición por lo general organizan las mediciones por parte y por operador. Sin embargo, el estudio R&R expandido del sistema de medición permite graficar otros factores.
En la gráfica, los puntos representan las mediciones y los símbolos de cruz en un círculo representan las medias. La línea de conexión conecta las mediciones promedio para cada nivel del factor.
Nota
Si hay más de 9 observaciones por nivel, Minitab muestra una gráfica de caja en lugar de una gráfica de valores individuales.
Interpretación
Cuando cada parte tiene múltiples mediciones que varían lo menos posible (los puntos correspondientes a una parte están juntos), significa que el sistema de medición presenta poca variación. Además, las mediciones promedio de las partes deberían variar lo suficiente como para indicar que las partes son diferentes y representan todo el rango del proceso.
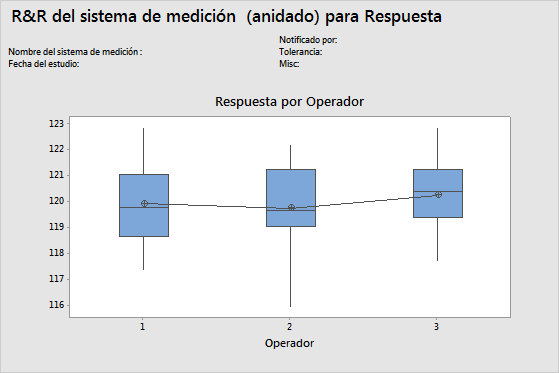
Gráfica Por operador
La gráfica Por operador muestra todas las mediciones que se tomaron en el estudio, organizadas por operador. Esta gráfica muestra las diferencias entre los niveles de los factores. Los estudios R&R del sistema de medición por lo general organizan las mediciones por parte y por operador. Sin embargo, el estudio R&R expandido del sistema de medición permite graficar otros factores.
Nota
Si hay más de 9 observaciones por operador, Minitab muestra una gráfica de caja en lugar de una gráfica de valores individuales.
Interpretación
Una línea horizontal recta entre los operadores indica que las medias de las mediciones de cada operador son similares. Lo ideal es que las mediciones de cada operador varíen en igual cantidad.