En este tema
Sesgo
El sesgo es la diferencia entre el valor de referencia de la parte y las mediciones de la parte realizadas por el operador.
Fórmula
Sesgo promedio de cada parte:
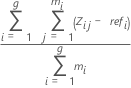
Notación
| Término | Description |
|---|---|
| zi,j | jésima medición de la iésima parte |
| refi | valor de referencia de la iésima parte |
| mi | número de réplicas de la iésima parte |
%Sesgo
El %Sesgo es el sesgo expresado como un porcentaje de la variación general del proceso.
Fórmulas
%Sesgo = 100 * (|Sesgo promedio| / Variación del proceso)
Notación
| Término | Description |
|---|---|
| zi,j | jésima medición de la iésima parte |
| refi | valor de referencia de la iésima parte |
| mi | número de réplicas de la iésima parte |
Valor p para Estudio de linealidad y sesgo del sistema de medición
Utilice los valores p para probar si el sesgo es igual a 0 en cada valor de referencia y si el sesgo promedio es igual a 0.
El valor p se define como el área por debajo de la distribución muestral a la derecha del |estadístico de prueba| positivo y el área por debajo de la distribución muestral a la izquierda del |estadístico de prueba| negativo. El valor p indicado en la salida se obtiene utilizando la distribución t con γ gl y el estadístico t.
Minitab proprociona cálculos específicos del estadístico t para el método basado en el rango de la muestra y para el método basado en la desviación estándar de la muestra.
Método basado en el rango de la muestra
Minitab utiliza el rango de la muestra (opción predeterminada) o la desviación estándar de la muestra para estimar la desviación estándar de la repetibilidad. La desviación estándar de la repetibilidad se utiliza para calcular el valor t, que conduce al cálculo del valor p para probar si el sesgo es igual a 0 para todos los valores de referencia y para cada referencia.
Fórmulas
Para el método que se basa en el rango de la muestra, cuando cada valor de referencia distinto corresponde a una única parte, la desviación estándar de la repetibilidad es:
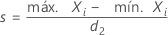
Cuando más de una parte tiene el mismo valor de referencia, la desviación estándar de la repetibilidad es:

El estadístico t para probar el sesgo es:

Los grados de libertad (γ) se obtienen a partir de una tabla del AIAG incluida en el manual 1. Minitab utiliza la distribución t con γ gl y el valor t para calcular el valor p.
Notación
| Término | Description |
|---|---|
| Xi | el sesgo de la medición iésima para una parte |
| d2 | un valor tomado de una tabla1, con tamaño de la muestra = n |
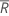 | rango promedio |
Método basado en la desviación estándar de la muestra
Minitab utiliza el rango de la muestra (opción predeterminada) o la desviación estándar de la muestra para estimar la desviación estándar de la repetibilidad. La desviación estándar de la repetibilidad se utiliza para calcular el valor t, que conduce al cálculo del valor p para probar si el sesgo es igual a 0.
Fórmulas
Para el método que se basa en la desviación estándar de la muestra, cuando un valor de referencia corresponde a una única parte, la desviación estándar de la repetibilidad es:

El estadístico t para probar el sesgo es:

Los grados de libertad son n - 1. El valor p indicado en la salida se obtiene de la distribución t usando el valor t y los grados de libertad.
Cuando más de una parte tiene el mismo valor de referencia, la desviación estándar de la repetibilidad es la desviación estándar agrupada de la muestra (s) para todas las partes que tienen el mismo valor de referencia:

El estadístico t para probar el sesgo es:

Los grados de libertad son (n1- 1) + ... + (ng - 1). El valor p indicado en la salida se obtiene de la distribución t usando el valor t y los grados de libertad.
Notación
| Término | Description |
|---|---|
| x | iésima medición de la parte |
 | medición promedio para cada parte |
| n | tamaño de la muestra |
| S1 | la desviación estándar para la parte 1 con n1 mediciones |
| Sg | la desviación estándar para la parte g con ng mediciones |
