En este tema
Gráfica Sesgo vs. valor de referencia
Utilice la gráfica Sesgo vs. valor de referencia para ver cómo varían los valores de sesgo para cada parte. Los puntos azules representan los valores de sesgo para cada valor de referencia. Los cuadrados rojos representan el valor promedio de sesgo para cada valor de referencia. La línea es el ajuste de la línea de regresión de mínimos cuadrados al promedio de las desviaciones.
Interpretación
La situación ideal es que las desviaciones de cada parte estén cerca de 0 y que la línea ajustada sea horizontal.
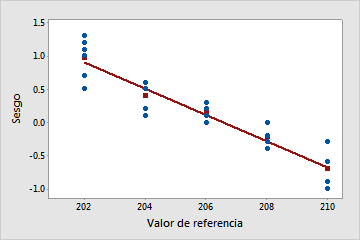
La linealidad parece ser un problema
La línea trazada presenta inclinación. En este ejemplo, las mediciones de las partes más pequeñas son mayores que los valores correspondientes de sus partes de referencia. Las mediciones de las partes más grandes tienden a ser menores que los valores correspondientes de sus partes de referencia.
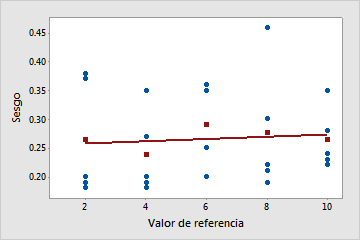
La linealidad no parece ser un problema
La línea trazada es casi una línea horizontal, lo que indica que el sesgo promedio es relativamente constante y no depende del valor de referencia. En este ejemplo, las mediciones de todas las partes son mayores que las mediciones correspondientes de sus partes de referencia.
Coef
Los coeficientes son números de la línea de regresión de la gráfica Sesgo vs. valor de referencia.
La forma general de esta línea de regresión de mínimos cuadrados es:
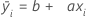
El término b representa el coeficiente de la constante. Indica el punto en el que la línea ajustada cruza el eje Y.
El término a representa el coeficiente de la pendiente. La pendiente de una línea indica la inclinación de la línea y es el cambio en el eje Y sobre el cambio en el eje X.
Interpretación
Cuando el coeficiente de la pendiente, a, es muy pequeño, la pendiente está cerca de la horizontal. Por lo tanto, el sesgo es relativamente constante para todos los valores de referencia y la linealidad no es un problema significativo. Valores absolutos más altos del coeficiente de la pendiente, |a|, indican una pendiente más pronunciada de la línea. Si el valor p de la pendiente es menor que alfa, entonces la linealidad es significativa.
En ausencia de linealidad significativa, valores absolutos más altos del coeficiente de la constante, |b|, indican un sesgo más grande. Cuando existe linealidad significativa, debe examinar los valores individuales de sesgo.
EE Coef
El error estándar de la estimación de un coeficiente de regresión mide la precisión con la que el modelo estima el valor desconocido del coeficiente. El error estándar del coeficiente siempre es positivo.
Interpretación
Utilice el error estándar del coeficiente para medir la precisión de la estimación del coeficiente. Cuanto menor sea el error estándar, más precisa será la estimación. Al dividir el coeficiente entre su error estándar se calcula un valor t. Si el valor p asociado con el valor t es menor que el nivel de significancia (α), usted concluye que el coeficiente es significativamente diferente de 0.
Valor p para la linealidad del sistema de medición
- P para la constante: Utilice este valor para probar si la constante de la línea de linealidad es igual a 0.
- P para la pendiente: Utilice este valor para probar si la pendiente de la línea de linealidad es igual a 0.
Interpretación
- Para la constante, si el valor p es mayor que el valor de α, usted no puede rechazar la hipótesis nula y concluye que el sesgo para todos los valores de referencia es igual a 0.
- Para la pendiente, si el valor p es mayor que el valor de α, usted no puede rechazar la hipótesis nula y concluye que el sistema de medición tiene el mismo sesgo para todos los valores de referencia (no hay linealidad).
- Para la constante, si el valor p es menor que el valor de α, usted rechaza la hipótesis nula y concluye que el sesgo para todos los valores de referencia no es igual a 0.
- Para la pendiente, si el valor p es menor que el valor de α, usted rechaza la hipótesis nula y concluye que el sistema de medición no tiene el mismo sesgo para todos los valores de referencia (hay linealidad).
S y R-cuad.
S y R-cuad. (R2) son mediciones de qué tan bien el modelo se ajusta a los datos.
S es una estimación de σ, la desviación estándar alrededor de la línea de regresión.
R-cuad. (R2) representa la proporción de variación en el sesgo que es explicada por la relación lineal entre los sesgos y los valores de referencia.
Interpretación
Los valores más bajos de S indican menos variabilidad en las estimaciones del sesgo. R2 varía de 0 a 100%. Por lo general, mientas mayor sea el valor de R2, mejor se ajustará el modelo a los datos.
Linealidad, %Linealidad
La linealidad evalúa la diferencia en el sesgo promedio en todo el rango esperado de operación del sistema de medición. La linealidad indica si el sistema de medición tiene la misma exactitud (el mismo sesgo) para todos los valores de referencia.
El %Linealidad es la linealidad expresada como un porcentaje de la variación del proceso.
Interpretación
Para interpretar la linealidad de los datos, determine si el sesgo cambia para los diferentes valores de referencia. Si los datos no forman una línea horizontal en una gráfica de dispersión, existe linealidad. Lo ideal es que la línea ajustada sea horizontal y esté cerca de 0.

La linealidad parece ser un problema
La línea trazada presenta inclinación. En este ejemplo, las mediciones de las partes más pequeñas son mayores que los valores correspondientes de sus partes de referencia. Las mediciones de las partes más grandes tienden a ser menores que los valores correspondientes de sus partes de referencia.

La linealidad no parece ser un problema
La línea trazada es casi una línea horizontal, lo que indica que el sesgo promedio es relativamente constante y no depende del valor de referencia. En este ejemplo, las mediciones de todas las partes son mayores que las mediciones correspondientes de sus partes de referencia.
Para un sistema de medición que mida las partes consistentemente, el %linealidad estará cerca de 0.
Sesgo, %Sesgo
El sesgo se calcula como la diferencia entre el valor estándar conocido de una parte de referencia y la medición promedio observada.El sesgo es una medida de la exactitud del sistema de medición.
El %Sesgo es el sesgo expresado como un porcentaje de la variabilidad del proceso.
Interpretación
- Un sesgo positivo indica que el sistema de medición mide por encima del valor real.
- Un sesgo negativo indica que el sistema de medición mide por debajo del valor real.
Para un sistema de medición que mida con exactitud, el %Sesgo será bajo.
Valor p para el sesgo del sistema de medición
- P para el sesgo promedio: Utilice este valor para probar si el sesgo promedio es igual a 0.
- P para cada valor de referencia: Utilice este valor para probar si el sesgo es igual a 0 en cada valor de referencia.
Interpretación
- Para cada valor de referencia, si el valor p es mayor que el valor de α, usted no puede rechazar la hipótesis nula y concluye que el sesgo es igual a 0.
- Para el sesgo promedio, si el valor p es mayor que el valor de α, usted rechaza la hipótesis nula y concluye que el sesgo promedio es igual a 0.
- Para cada valor de referencia, si el valor p es menor que el valor de α, usted rechaza la hipótesis nula y concluye que el sesgo no es igual a 0.
- Para el sesgo promedio, si el valor p es menor que el valor de α, usted rechaza la hipótesis nula y concluye que el sesgo promedio no es igual a 0.
