En este tema
Componentes de la varianza
La gráfica Contribución de los componentes de la varianza y la tabla Componentes de la varianza muestran la variación de diferentes fuentes.
Interpretación
Utilice los componentes de varianza para evaluar la variación de cada origen. La varianza prueba-reprueba y la varianza del operador son errores de medición. La variación de partes representa el rango de partes del estudio. La varianza total es la suma de los demás componentes. Si el análisis incluye la interacción, entonces la cantidad de error de medición depende de la parte que mide un operador.
En un sistema de medición aceptable, el mayor componente de la variación es la variación de la parte. Si la variación prueba-reprueba y la variación del operador contribuyen a grandes cantidades de variación, investigue el origen del problema y tome medidas correctivas.
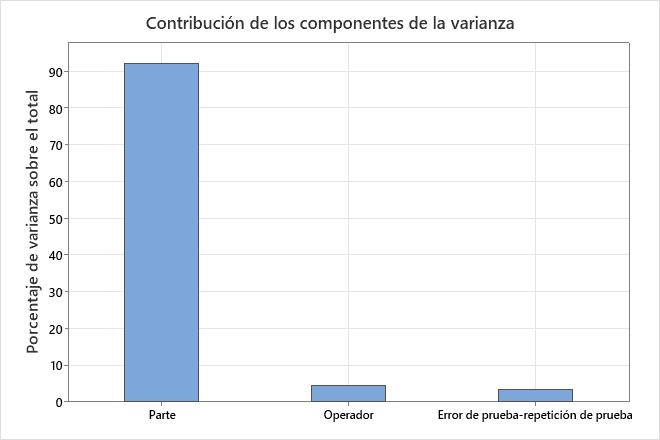
Componentes de la varianza
| Fuente | Varianza | %Total | DesvEst |
|---|---|---|---|
| Error de prueba-repetición de prueba (repetibilidad) | 0.03997 | 3.394 | 0.19993 |
| Operador (Reproducibilidad) | 0.05146 | 4.368 | 0.22684 |
| Parte (Variación del producto) | 1.08645 | 92.238 | 1.04233 |
| Total | 1.17788 | 100.000 | 1.08530 |
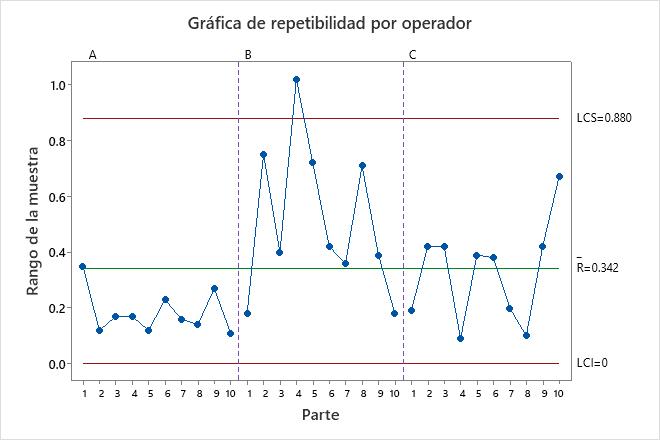
Gráfica de repetibilidad
La gráfica de repetibilidad es un gráfico de control de rangos que muestra la coherencia del operador.
- Puntos graficados
- Para cada operador, el rango de muestra es la diferencia entre las medidas más grandes y más pequeñas de cada parte. Utilice los rangos de muestra para evaluar la coherencia del operador.
- Línea central (Rbarra)
- El promedio general del proceso (es decir, el promedio de todos los rangos de muestras).
- Límites de control (LCI y LCS)
- La cantidad de variación que usted puede esperar para los rangos de las muestras. Para calcular los límites de control, Minitab utiliza la variación de cada muestra.
Nota
Si cada operador mide cada pieza 9 veces o más, Minitab muestra las desviaciones estándar en la gráfica en lugar de rangos.
Interpretación
Cuanto menor sea el rango promedio, menor será la variación del sistema de medición. Un punto mayor que el límite de control superior (LCS) indica que el operador no mide las partes consistentemente. El cálculo del LCS incluye el número de mediciones por pieza por parte de cada operador y la variación de la pieza. Si los operadores miden las partes consistentemente, entonces el rango entre las mediciones máxima y mínima es pequeña, en relación con la variación del estudio, y los puntos deberían estar bajo control.
Gráfica de señal a ruido por operador
El gráfico compara la variación de la parte con el componente de prueba-reprueba.
- Puntos graficados
- La medición promedio de cada parte, graficada para cada operador.
- Línea central (
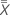 )
) - El promedio general para todas las mediciones de las partes realizadas por todos los operadores.
- Límites de control (LCI y LCS)
- Los límites de control se basan en la estimación de la repetibilidad y el número de mediciones en cada promedio.
Interpretación
Las partes que se eligen para un estudio deben representar toda la gama de partes posibles. Por lo tanto, este gráfico debería indicar más variación entre los promedios de las partes de lo que se espera de la variación prueba-reprueba solamente.
En un escenario ideal, la gráfica tiene límites de control estrechos con muchos puntos fuera de control que indican un sistema de medición con poca variación.
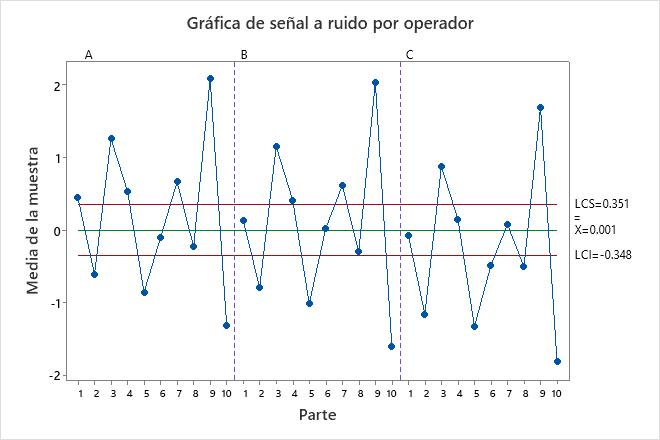
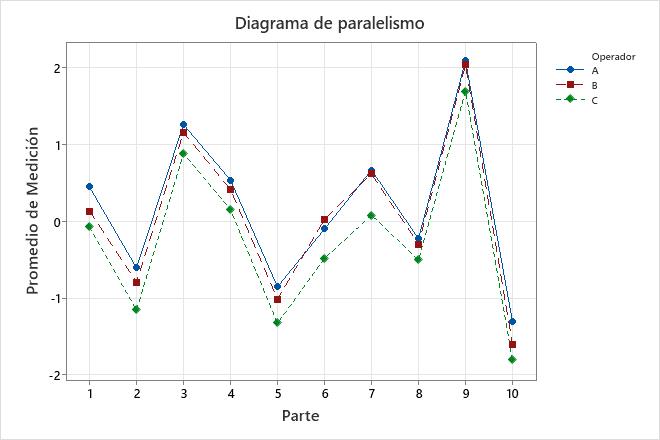
Diagrama de paralelismo
El diagrama de paralelismo muestra las mediciones medias de cada operador para cada parte. Cada línea conecta los promedios de un mismo operador.
El diagrama muestra la interacción entre dos fuentes de variación: las partes y los operadores. Una interacción ocurre cuando el efecto de un factor depende de un segundo factor.
Interpretación
Las líneas que son coincidentes indican que los operadores miden de manera similar. Las líneas que no son paralelas o que se cruzan indican que la capacidad de un operador para medir una parte de manera consistente depende de la parte que se está midiendo. Una línea que es consistentemente más alta o más baja que las demás indica que un operador agrega sesgo a la medición al realizar mediciones consistentemente altas o bajas.
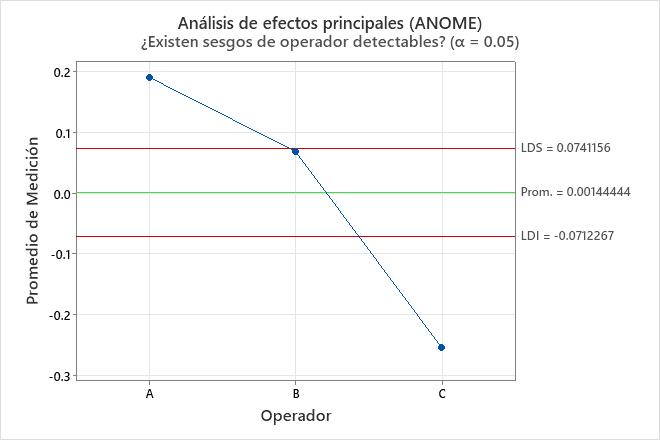
Gráfica de análisis de efectos principales (ANOME)
La gráfica compara las mediciones medias de los operadores.
- Puntos graficados
- La medida media de todas las piezas para cada operario.
- Línea central (promedio)
- El promedio general para todas las mediciones de las partes realizadas por todos los operadores.
- Límites de decisión (LDL y UDL)
- Los límites se basan en la estimación prueba-reprueba y en el número de mediciones en cada promedio.
Interpretación
Los puntos fuera de los límites de decisión indican que diferentes operadores añaden sesgo a las mediciones. Idealmente, los puntos están todos dentro de los límites de decisión para indicar que los promedios generales de los operadores son similares.
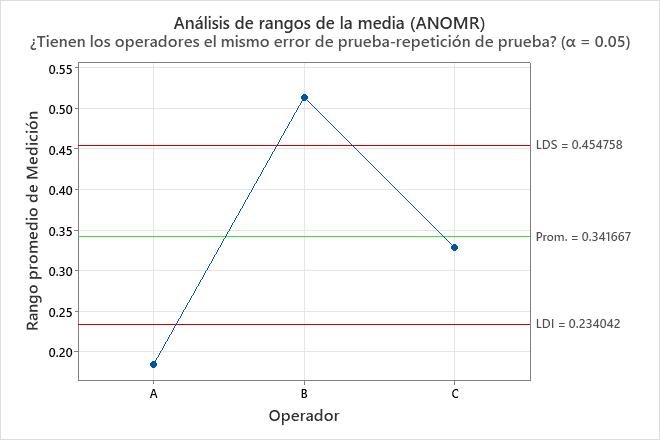
Gráfica de análisis de rangos medios (ANOMR)
La gráfica compara el rango promedio de mediciones para los operadores.
- Puntos graficados
- El promedio de los rangos de las medidas para cada parte para cada operador.
- Línea central (promedio)
- El promedio general de todos los rangos por todos los operadores.
- Límites de decisión (LDL y UDL)
- Los límites se basan en la estimación de la prueba-reprueba.
Interpretación
Los puntos fuera de los límites de decisión indican que algunos operadores miden de manera más o menos consistente que otros operadores. Idealmente, todos los puntos están dentro de los límites de decisión para indicar que los rangos generales de los operadores son similares.
Estadísticas EMP y pautas de clasificación
Las estadísticas EMP clasifican el sistema de medición desde la mejor calificación de Primera Clase hasta la peor calificación de Cuarta Clase. Las clases corresponden al coeficiente de correlación intraclase. En términos prácticos, el coeficiente explica qué tan bien el sistema de medición detecta un cambio en la media del proceso de al menos 3 desviaciones estándar. Los sistemas de medición de primera y segunda clase suelen tener una alta probabilidad de detectar tales cambios con un número limitado de pruebas y subgrupos en un gráfico de control. Para los sistemas de medición de tercera clase, el análisis típico agrega pruebas al gráfico de control para aumentar la probabilidad de detectar un cambio en la media del proceso. Un sistema de medición de cuarta clase generalmente requiere mejoras para monitorear un proceso o para actividades de mejora de procesos.
La clasificación también se relaciona con la atenuación de las señales del proceso. La atenuación es la cantidad de cambio que se confunde con el error de medición. Para un sistema de medición que atenúa el 50% de un cambio, es probable que un cambio de 2 desviaciones estándar aparezca como un cambio de 1 desviación estándar.
- Error de prueba-reprueba
- La variabilidad en las mediciones cuando el mismo operador mide la misma parte varias veces. Cuanto menor sea el valor, mejor será el rendimiento del sistema de medición.
- Grados de libertad
- Los grados de libertad (DF) para la estimación del error prueba-reprueba. En general, DF mide cuánta información está disponible para calcular el error.
- Error probable
- La incertidumbre para una sola medición. El análisis compara el error probable con el incremento de medición en la tabla Resolución efectiva de mediciones para concluir si la precisión de las mediciones es confiable. Wheeler (2006) 1 Describe los métodos para utilizar el error probable para determinar los límites de especificación de un proceso, dado el rendimiento del sistema de medición.
- Correlación intraclase
- El coeficiente de correlación intraclase compara la variación total con la variación parcial. Los valores más cercanos a 1 indican menos variación con respecto al sistema de medición.
- Sin sesgos
- Sin sesgo, el coeficiente describe qué tan bien funciona el sistema de medición si todos los operadores miden las piezas de la misma manera en promedio.
- Con sesgo
- Con el sesgo, el coeficiente describe qué tan bien funciona el sistema de medición con diferencias entre operadores.
- Con sesgo e interacción
- Cuando el análisis detecta que diferentes operadores miden diferentes partes de manera diferente, entonces los resultados incluyen la correlación intraclase con el sesgo y la interacción. El coeficiente describe qué tan bien funciona el sistema de medición cuando diferentes operadores miden diferentes partes de manera diferente.
- Impacto del sesgo
- La diferencia entre el coeficiente intraclase con sesgo y sin sesgo. Cuanto menor sea el valor, menos contribuirán las diferencias de operador a la variación de las mediciones.
- Sesgo e impacto de la interacción
- La diferencia entre el coeficiente intraclase con sesgo e interacción y el coeficiente sin sesgo. Cuanto menor sea el valor, menos contribuirán las diferencias en la forma en que los diferentes operadores miden las diferentes partes a la variación en las mediciones.
Estadísticas de EMP
| Estadísticas | Valor | Clasificación |
|---|---|---|
| Error de prueba-repetición de prueba | 0.1999 | |
| Grados de libertad | 78.0000 | |
| Error probable | 0.1349 | |
| Correlación intraclase (sin sesgo) | 0.9645 | Primera clase |
| Correlación intraclase (con sesgo) | 0.9224 | Primera clase |
| Impacto del sesgo | 0.0421 |
Directrices de clasificación
| Clasificación | Correlación intraclase | Atenuación de las señales de proceso | Probabilidad de advertencia, Prueba 1* | Probabilidad de advertencia, Pruebas* |
|---|---|---|---|---|
| Primera clase | 0.80 - 1.00 | Menos de 11% | 0.99 - 1.00 | 1.00 |
| Segunda clase | 0.50 - 0.80 | 11 - 29% | 0.88 - 0.99 | 1.00 |
| Tercera clase | 0.20 - 0.50 | 29 - 55% | 0.40 - 0.88 | 0.92 - 1.00 |
| Cuarta clase | 0.00 - 0.20 | Más de 55% | 0.03 - 0.40 | 0.08 - 0.92 |
Resolución efectiva de mediciones
Las estadísticas sobre la resolución describen cuánto puede confiar en la precisión registrada de las mediciones.
- Error probable (PE)
- La incertidumbre para una sola medición. El análisis compara el error probable con el incremento de medición en la tabla Resolución efectiva de mediciones para concluir si la precisión de las mediciones es confiable. Wheeler (2006)1 describe métodos para utilizar el error probable para determinar los límites de especificación de un proceso, dado el rendimiento del sistema de medición.
- Límite inferior de incremento (0,1 * PE)
- Un límite inferior para cuando el incremento de medición es confiable. Cuando el incremento de medición es menor que el límite inferior del incremento, considere seriamente si desea registrar las mediciones con menos precisión.
- Incremento efectivo más pequeño (0,22 * PE)
- Una estimación de la precisión de la medición que es probable que produzca el sistema. Cuando el incremento de medición es menor que el incremento efectivo más pequeño, considere si desea registrar las mediciones con menos precisión.
- Incremento de medición actual
- Una estimación a partir de los datos o un valor especificado que explica la precisión de las mediciones registradas. Por ejemplo, para los valores 1,1; 1,4 y 1,9, el análisis determina que el incremento es 0,1 porque las mediciones incluyen el lugar de las décimas.
- Incremento efectivo más grande (2,2 * PE)
- Una estimación de la precisión de la medición que es probable que produzca el sistema. Cuando el incremento de medición es mayor que el incremento efectivo más grande, considere si desea registrar las mediciones con más precisión.
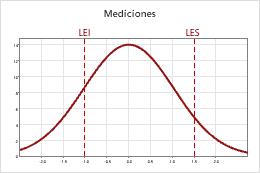
Probabilidades de clasificación errónea
Cuando se especifica por lo menos un límite de especificación, Minitab puede calcular las probabilidades de que se realice una clasificación errónea de un producto. Debido a la variación del sistema de medición, el valor medido de la parte no siempre es igual al valor real de la parte. La discrepancia entre el valor medido y el valor real crea el potencial para clasificar erróneamente la parte.
- Probabilidad conjunta
- Utilice la probabilidad conjunta cuando no tenga conocimiento previo sobre la aceptabilidad de las partes. Por ejemplo, usted toma una muestra de una línea de producción y no sabe si cada parte específica es una parte buena o mala. Hay dos tipos de clasificación errónea que pueden ocurrir:
- La probabilidad de que la parte esté mala y usted la acepte.
- La probabilidad de que la parte esté buena y usted la rechace.
- Probabilidad condicional
- Utilice la probabilidad condicional cuando tenga conocimiento previo sobre la aceptabilidad de las partes. Por ejemplo, usted toma una muestra de una pila de unidades reparadas o de una pila de productos que pronto se enviarán como partes buenas. Hay dos tipos de clasificación errónea que pueden ocurrir:
- La probabilidad de que usted acepte una parte seleccionada de una pila de productos malos que deben repararse (también conocida como falsa aceptación).
- La probabilidad de que usted rechace una parte seleccionada de una pila de productos buenos que están a punto de ser enviados (también conocida como falso rechazo).
Interpretación
Probabilidades conjuntas de clasificación errónea
| Descripción | Probabilidad |
|---|---|
| Se aceptó una parte seleccionada aleatoriamente que está en mal estado | 0.037 |
| Se rechazó una parte seleccionada aleatoriamente que está en buen estado. | 0.055 |
Probabilidades condicionales de clasificación errónea
| Descripción | Probabilidad |
|---|---|
| Se aceptó una parte proveniente de un grupo de productos en mal estado | 0.151 |
| Se rechazó una parte proveniente de un grupo de productos en buen estado | 0.073 |
La probabilidad conjunta de que una parte esté mala y usted la acepte es de 0,037. La probabilidad conjunta de que una parte esté buena y usted la rechace es de 0,055.
La probabilidad condicional de una falsa aceptación, que usted acepte una parte durante la reinspección cuando realmente está fuera de las especificaciones, es de 0,151. La probabilidad condicional de un falso rechazo, que usted rechace una parte durante la reinspección cuando realmente está dentro de las especificaciones, es de 0,073.
