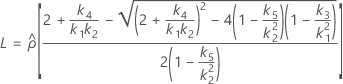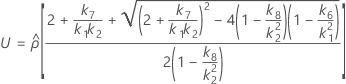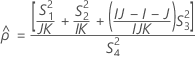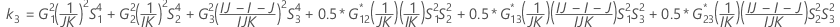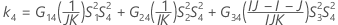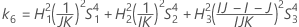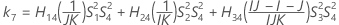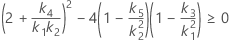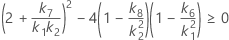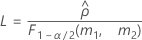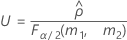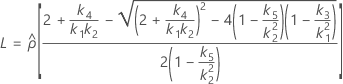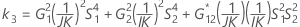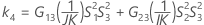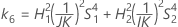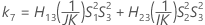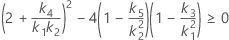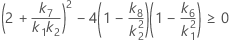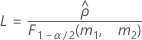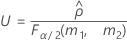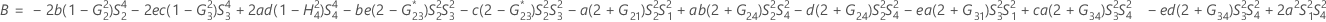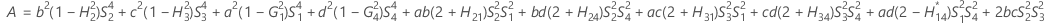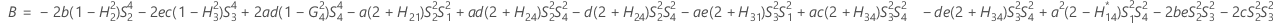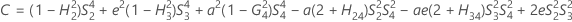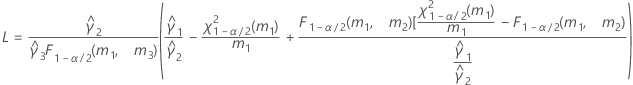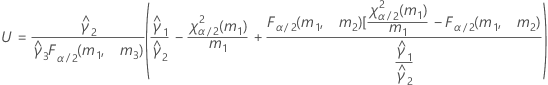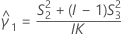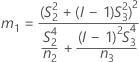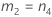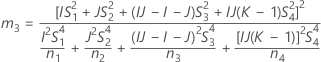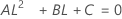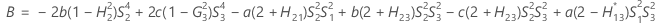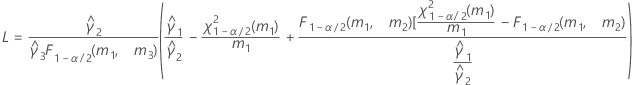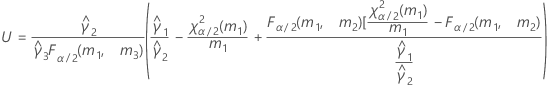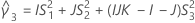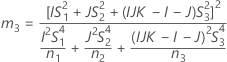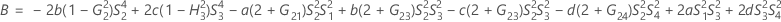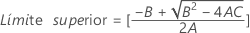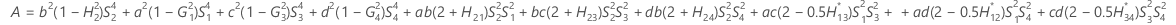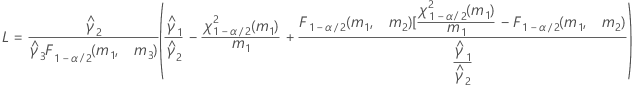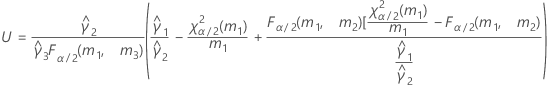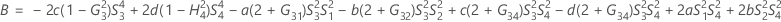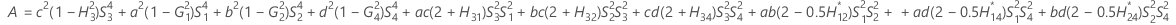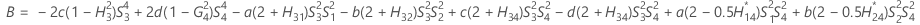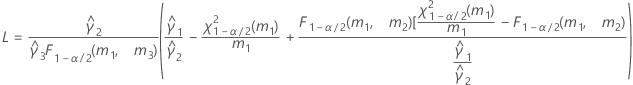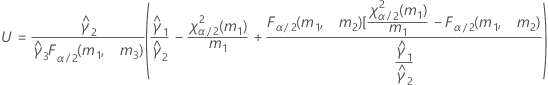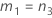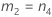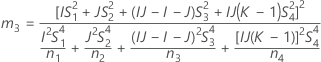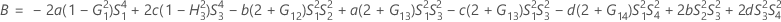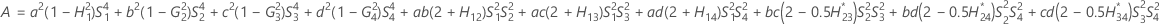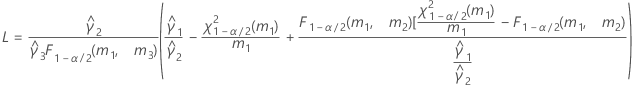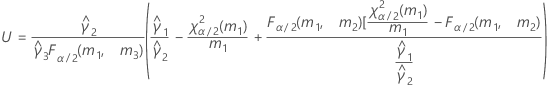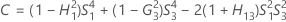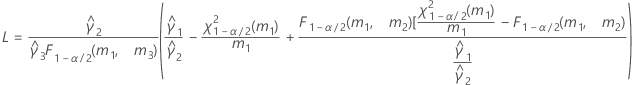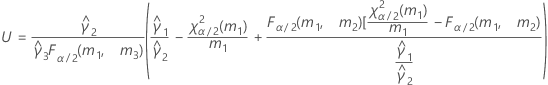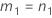En este tema
- Intervalo de confianza para la relación de la varianza de la repetibilidad y la varianza total
- Intervalo de confianza para la relación de la varianza de la reproducibilidad y la varianza total
- Intervalo de confianza para la relación de la varianza del operador y la varianza total
- Intervalo de confianza para la relación de la varianza de la interacción y la varianza total
- Intervalo de confianza para la relación de la varianza de la parte y la varianza total
- Intervalo de confianza para la relación de la varianza del sistema de medición y la varianza total
Intervalo de confianza para la relación de la varianza de la repetibilidad y la varianza total
Con operador
Cuando se incluye el término Operador y término de interacción, existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza la aproximación de Satterthwaite. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
-

- Aproximación de Satterthwaite
- Las fórmulas para los límites inferior y superior siguen siendo válidas, excepto por el hecho de que L y U se definen de la siguiente manera:
Con término Operador


Sin término de interacción
Cuando se incluye el término Operador y término de interacción, existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza la aproximación de Satterthwaite. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
-

- Aproximación de Satterthwaite
- Las fórmulas para los límites inferior y superior siguen siendo válidas, excepto por el hecho de que L y U se definen de la siguiente manera:
Notación
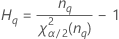
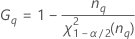
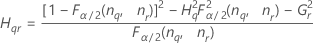
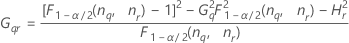
| Término | Description |
|---|---|
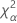 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza para la relación de la varianza de la reproducibilidad y la varianza total
Con término de interacción
Existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza una aproximación alternativa. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1- α) * 100% se calculan resolviendo ecuaciones cuadráticas.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Sin término de interacción
Existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza una aproximación alternativa. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan resolviendo ecuaciones cuadráticas. El límite inferior, L, es igual a J veces la solución más pequeña para la siguiente ecuación.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Notación
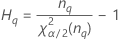
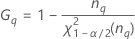
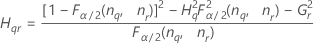
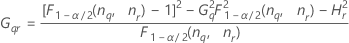
| Término | Description |
|---|---|
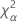 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
| a | I |
| b | J |
| c | (IJ – I –J) |
| d | IJ(K-1) |
| e | I – 1 |
Intervalo de confianza para la relación de la varianza del operador y la varianza total
Existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza una aproximación alternativa. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan resolviendo ecuaciones cuadráticas.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Notación
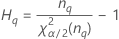
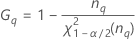
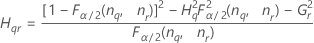
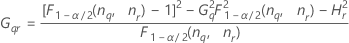
| Término | Description |
|---|---|
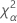 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza para la relación de la varianza de la interacción y la varianza total
Existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza una aproximación alternativa. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan resolviendo ecuaciones cuadráticas.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Notación
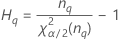
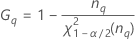
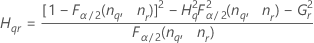
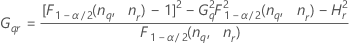
| Término | Description |
|---|---|
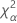 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza para la relación de la varianza de la parte y la varianza total
Con operador y término de interacción
Existen dos métodos de cálculo posibles. En primer lugar, Minitab calcula los límites usando el método modificado para muestras grandes (MLS, por sus siglas en inglés). Si no se cumplen ciertas condiciones durante los cálculos, Minitab utiliza una aproximación alternativa. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan resolviendo ecuaciones cuadráticas.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Con término Operador
Límite inferior = 1 – (el límite inferior de la relación de la varianza de la repetibilidad y la varianza total)
Límite superior = 1 – (el límite superior de la relación de la varianza de la repetibilidad y la varianza total)
Sin término de interacción
- Método MLS
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan resolviendo ecuaciones cuadráticas.
- Segundo método
- Los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100% se calculan de la siguiente manera:
Notación
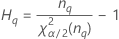
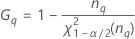
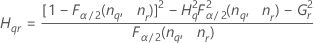
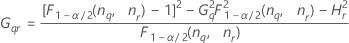
| Término | Description |
|---|---|
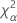 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza para la relación de la varianza del sistema de medición y la varianza total
Límite inferior = 1 – (límite inferior del IC de la relación de la varianza de la parte y la varianza total)
Límite superior = 1 – (límite superior del IC de la relación de la varianza de la parte y la varianza total)