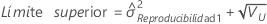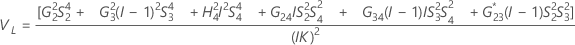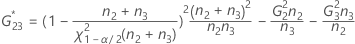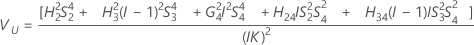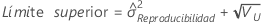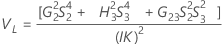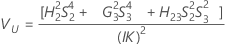En este tema
- Notación común y reglas para los intervalos de confianza del estudio R&R del sistema de medición
- Intervalo de confianza del componente de la varianza Repetibilidad
- Intervalo de confianza del componente de la varianza de Reproducibilidad (u Operador)
- Intervalo de confianza del componente de la varianza Operador
- Intervalo de confianza del componente de la varianza Interacción
- Intervalo de confianza de los componentes de la varianza total del sistema de medición
- Intervalo de confianza del componente de la varianza Entre las partes
- Intervalo de confianza de los componentes de la varianza total
Notación común y reglas para los intervalos de confianza del estudio R&R del sistema de medición
Para todos los componentes de la varianza, los bordes inferior y superior de los componentes de la varianza no deben ser valores negativos. Si los bordes calculados usando las fórmulas son negativos, entonces se establecen en cero.
Para todas las relaciones entre 0 y 1, los bordes inferior y superior también deben estar entre 0 y 1. Si los bordes están fuera del rango, se establecen en 0 o 1 según corresponda.
Notación
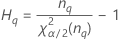
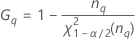
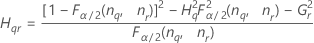
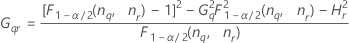
| Término | Description |
|---|---|
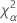 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| Fα(nq, nγ) | el percentil α *100 de la distribución F con nq y nγ grados de libertad |
| I | el número de partes |
| J | el número de operadores |
| K | el número de réplicas |
Los grados de libertad:
Partes: n1=I–1
Operadores: n2=J–1
Partes*Operadores: n3=(I–1)(J–1)
Réplicas: n4=IJ(K–1)
MSParte = S12
MSOperador = S22
MSParte*Operador = S32
MSRéplicas = S34
Intervalo de confianza del componente de la varianza Repetibilidad
Minitab calcula los límites inferior y superior de un intervalo de confianza exacto de (1 – α) *100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Fórmulas
- Con operador
-

- Sin operador
-

- Sin término de interacción
-

Notación
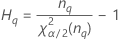
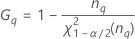
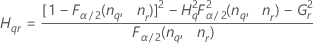
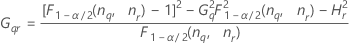
| Término | Description |
|---|---|
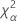 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza del componente de la varianza de Reproducibilidad (u Operador)
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Fórmulas
- Con término de interacción
-
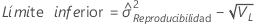
- Sin término de interacción
-
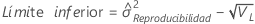
Notación
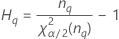
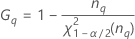
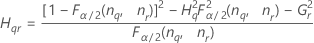
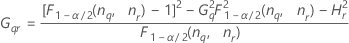
| Término | Description |
|---|---|
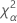 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza del componente de la varianza Operador
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1–α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Fórmulas


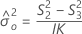
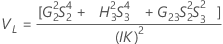
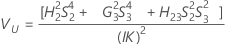
Notación
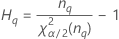
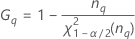
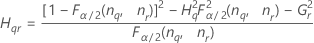
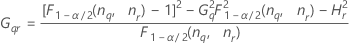
| Término | Description |
|---|---|
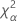 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza del componente de la varianza Interacción
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Fórmulas


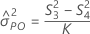

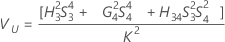
Notación
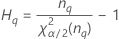
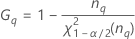
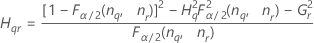
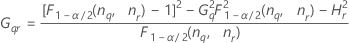
| Término | Description |
|---|---|
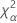 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza de los componentes de la varianza total del sistema de medición
Con operador y término de interacción
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.



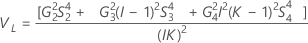
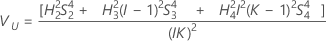
Con término Operador
Los límites inferior y superior de un intervalo de confianza exacto de (1 – α) *100% son:


Sin término de interacción
Minitab utiliza el método modificado para muestras grandes (MLS), los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) *100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.



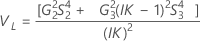
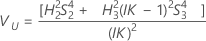
Notación
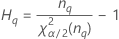
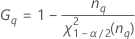
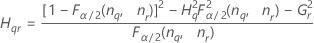
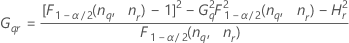
| Término | Description |
|---|---|
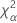 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza del componente de la varianza Entre las partes
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Con operador



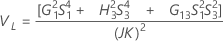
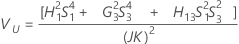
Sin operador


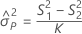
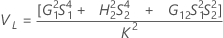
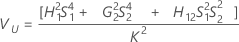
Sin interacción



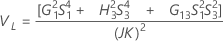
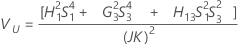
Notación
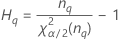
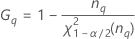
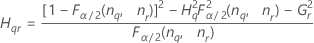
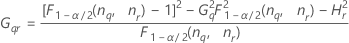
| Término | Description |
|---|---|
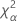 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |
Intervalo de confianza de los componentes de la varianza total
Minitab utiliza el método modificado para muestras grandes (MLS) para calcular los límites inferior y superior de un intervalo de confianza aproximado de (1 – α) * 100%. Para calcular los límites de confianza unilaterales, reemplace α/2 por α en H y G.
Con operador



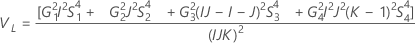
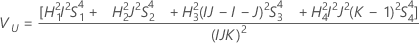
Sin operador


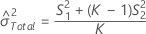
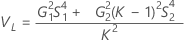
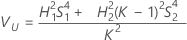
Sin término de interacción


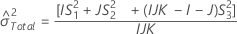
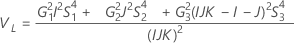
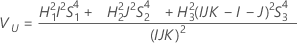
Notación
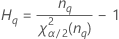
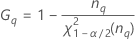
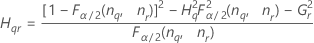
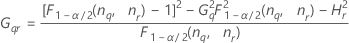
| Término | Description |
|---|---|
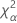 | el percentil α *100 de la distribución de chicuadrada con nq grados de libertad |
| J | el número de operadores |
| I | el número de partes |
| K | el número de réplicas |