En este tema
Sesgo
El sesgo se calcula como la diferencia entre el valor estándar conocido de una parte de referencia y la medición promedio observada.
- Estimación de puntos de sesgo con un límite inferior de tolerancia
- sesgo = límite inferior + intersección / pendiente
- Estimación de puntos de sesgo con un límite superior de tolerancia
- sesgo = límite superior + intersección / pendiente
La intersección y la pendiente de ambas fórmulas provienen de la línea ajustada de la gráfica de probabilidad.
Minitab hace la regresión de puntuación z Φ-1(Prob (Aceptación)) sobre los valores de referencia XT para calcular la intersección y la pendiente.
Repetibilidad preajustada
La repetibilidad preajustada es la repetibilidad que se calcula antes de ajustar para la sobrestimación.
Fórmula
Minitab estima la repetibilidad preajustada mediante:

Notación
| Término | Description |
|---|---|
| XT | representa los valores de referencia estimados con las probabilidades de aceptación de 0.995 y 0.005, que se calculan a partir de la línea ajustada en la gráfica de probabilidad. |
Repetibilidad
Repetibilidad es la cantidad de variación en el sistema de medición que se debe al instrumento de medición. Un estudio del sistema de medición por atributos hace una regresión de las probabilidades de aceptación sobre los valores de referencia para obtener la repetibilidad.
La repetibilidad preajustada es la repetibilidad que se calcula antes de ajustar para la sobrestimación. Minitab divide las estimaciones de repetibilidad entre el factor de ajuste 1.08 para calcular la repetibilidad ajustada.
Fórmula
Minitab estima la repetibilidad mediante:
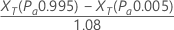
Notación
| Término | Description |
|---|---|
| XT | representa los valores de referencia estimados con las probabilidades de aceptación de 0.995 y 0.005, que se calculan a partir de la línea ajustada en la gráfica de probabilidad. |
El denominador, 1.08, es el factor de ajuste proporcionado por el grupo Automotive Industry Action Group 1 Minitab utiliza el valor de repetibilidad ajustada para probar si sesgo = 0.
T para el método AIAG
Fórmula
Para probar si el sesgo es igual a 0 usando el método de regresión, Minitab utiliza la siguiente fórmula:
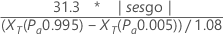
Notación
| Término | Description |
|---|---|
| XT | representa los valores de referencia estimados con las probabilidades de aceptación de 0.995 y 0.005, que se calculan a partir de la línea ajustada en la gráfica de probabilidad. |
- 6 partes que tienen aceptaciones mayores que 0 y menores que 20
- 1 parte tiene 0 aceptaciones
- 1 parte tiene 20 aceptaciones
T para el método de regresión
Fórmula
Para probar si el sesgo es igual a 0 usando el método de regresión, Minitab utiliza la siguiente fórmula:
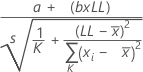
Notación
| Término | Description |
|---|---|
| a | la intersección de la línea ajustada de la gráfica de probabilidad |
| b | la pendiente de la línea ajustada de la gráfica de probabilidad |
| LL | límite inferior de tolerancia |
| s | la desviación estándar del error calculada usando la línea ajustada |
| K | el número de partes |
| xi | el valor de referencia de cada parte |
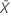 | la media de los valores de referencia |
GL para el método AIAG
Los grados de libertad se utilizan para calcular el valor p.
GL = N – 1.
Notación
| Término | Description |
|---|---|
| N | número de ensayos |
GL para el método de regresión
Los grados de libertad se utilizan para calcular el valor p.
GL = N – 2.
Notación
| Término | Description |
|---|---|
| N | número de puntos utilizados para obtener la línea ajustada |
Valor p
Los valores p se utilizan en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula.
Para determinar si el sesgo en el sistema de medición es estadísticamente significativo, compare el valor p con el nivel de significancia. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe sesgo cuando no hay ningún sesgo significativo.
Línea ajustada
Una línea ajustada es una línea de regresión que examina la relación entre la probabilidad de aceptaciones y los valores de referencia de las partes medidas.
La forma general de una línea ajustada es: Y = b0 + b1 X
Minitab hace la regresión de la puntuación z Φ-1(Prob (Aceptación)) sobre los valores de referencia XT para obtener la intersección y la pendiente.
Notación
| Término | Description |
|---|---|
| b0 | la intersección: la constante que determina la ubicación vertical de la línea de regresión. |
| b1 | la pendiente de la línea de regresión |
| X | los valores predictores |
R-cuad. para la línea ajustada
El R-cuad. para la línea ajustada es el coeficiente de determinación, que se utiliza para verificar si la línea ajustada modela adecuadamente los datos. El valor de R-cuad. (R2) para la línea de regresión ajustada indica que el porcentaje de la variación en las respuestas de probabilidad de aceptación que es explicado por el modelo de regresión.
R2 = 1 - (SC error / SC total)
Notación
| Término | Description |
|---|---|
| SC del error | suma de los cuadrados del error |
| SC total | suma total de los cuadrados |
