En este tema
Paso 1: Evaluar si hay sesgo en el sistema de medición
El sesgo es una medida de la exactitud del sistema de medición. El sesgo se calcula como la diferencia entre el valor estándar conocido de una parte de referencia y la medición promedio observada. Un valor de sesgo bajo indica que el sistema de medición de atributos mide las partes cerca de sus valores de referencia.
Para determinar si el sesgo en el sistema de medición es estadísticamente significativo, compare el valor p con el nivel de significancia. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe sesgo cuando no hay ningún sesgo significativo.
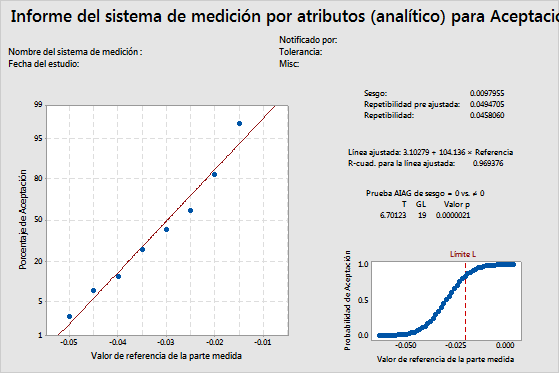
Resultado clave: Valor p
Para este ejemplo, el sesgo es 0.0097955 y el valor p es 0.0000021. Puesto que el valor p es menor que el nivel de significancia de 0.05, usted rechaza la hipótesis nula de que el sesgo es igual a 0. Usted concluye que el sesgo del sistema de medición es estadísticamente significativo.
Nota
Si cambia el valor predeterminado para utilizar el método de regresión en lugar del método AIAG, el valor p puede diferir ligeramente.
Paso 2: Evaluar la gráfica de línea ajustada
La gráfica de probabilidad normal muestra el porcentaje de aceptaciones para cada valor de referencia. Debido a que no se dispone de mediciones reales del sistema de medición para estimar el sesgo y la repetibilidad, Minitab calcula el sesgo y la repetibilidad al ajustar la curva de distribución normal utilizando las probabilidades calculadas de aceptación y los valores de referencia conocidos para todas las partes.
Si los errores de medición siguen una distribución normal, las probabilidades calculadas se sitúan a la largo de una línea recta. Una línea de regresión se ajusta a las probabilidades.
El valor de R-cuad. (R2) para la línea de regresión ajustada indica el porcentaje de la variación en las respuestas de probabilidad de aceptación que es explicado por el modelo de regresión. R2 varía de 0 a 100%. Por lo general, mientas mayor sea el valor de R2, mejor se ajustará el modelo a los datos. Los valores de R2 superiores a 90% normalmente indican un ajuste de los datos muy adecuado.

Resultado clave: R-cuad.
Para este ejemplo, el R-cuad. es 0.969376. La línea ajustada se ajusta muy bien a los datos y el modelo explica casi el 97% de la varianza.
Paso 3: Evaluar la curva de rendimiento del sistema de medición
La curva de rendimiento del sistema de medición indica la probabilidad estimada de aceptación en función del valor de referencia para el elemento. La línea de referencia vertical indica los límites que usted ingresó para el análisis.
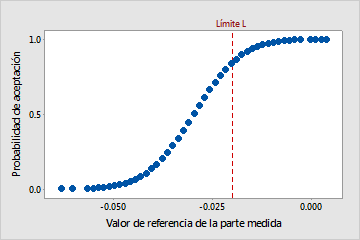
Para estos datos, la probabilidad de aceptar un elemento en el límite inferior de tolerancia de –0.020 es relativamente alta (aproximadamente 0.84). Sin embargo, la tasa de aceptación también es relativamente alta con valores apenas por debajo del límite de tolerancia. Si el límite inferior de tolerancia es crítico, entonces es necesario hacer algunas mejoras.
