En este tema
Sesgo
El sesgo es una medida de la exactitud del sistema de medición. El sesgo se calcula como la diferencia entre el valor estándar conocido de una parte de referencia y la medición promedio observada.
Interpretación
- Un sesgo positivo indica que el sistema de medición mide por encima del valor real.
- Un sesgo negativo indica que el sistema de medición mide por debajo del valor real.
Para un sistema de medición que mida con exactitud, el %sesgo será bajo. Para determinar si el sesgo es estadísticamente significativo, utilice el valor p.
Repetibilidad y repetibilidad preajustada
Repetibilidad es la cantidad de variación en el sistema de medición que se debe al instrumento de medición. Un estudio del sistema de medición por atributos hace una regresión de las probabilidades de aceptación sobre los valores de referencia para obtener la repetibilidad.
La repetibilidad preajustada es la repetibilidad que se calcula antes de ajustar para la sobrestimación. Minitab divide las estimaciones de repetibilidad entre el factor de ajuste 1.08 para calcular la repetibilidad ajustada. El factor de ajuste de 1.08 es proporcionado por Automotive Industry Action Group (AIAG) en 1.
Interpretación
Un valor bajo de repetibilidad indica que el sistema de medición mide de manera consistente. Un valor alto de repetibilidad indica variación aleatoria o problemas tales como una selección inadecuada de las partes o un sistema de medición deficiente.
Minitab utiliza el valor ajustado de repetibilidad en el cálculo para probar la hipótesis nula de que el sesgo es igual a 0.
Gráfica de probabilidad normal
La gráfica de probabilidad normal muestra el porcentaje de aceptaciones para cada valor de referencia. Debido a que no se dispone de mediciones reales del sistema de medición para estimar el sesgo y la repetibilidad, Minitab calcula el sesgo y la repetibilidad al ajustar la curva de distribución normal utilizando las probabilidades calculadas de aceptación y los valores de referencia conocidos para todas las partes.
Si los errores de medición siguen una distribución normal, las probabilidades calculadas se sitúan a la largo de una línea recta. Una línea de regresión se ajusta a las probabilidades.
Interpretación
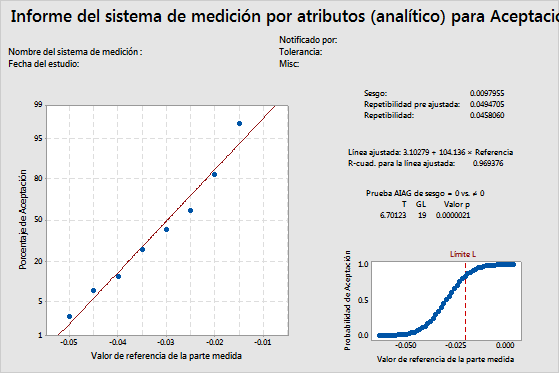
Línea ajustada
La probabilidad de aceptación para cada parte se calcula y se grafica en una gráfica de probabilidad normal. En una gráfica de probabilidad normal, el valorde Y de un punto graficado = Φ–1(Probabilidad de aceptación), donde Φ–1 es la inversa de la función de distribución acumulada normal estándar.
Una línea de regresión ajustada se dibuja a través de puntos graficados.
Interpretación
Si la línea ajustada representa un ajuste adecuado para los puntos graficados, Minitab utiliza los valores de intersección y pendiente para calcular los valores de sesgo y repetibilidad.

Esta gráfica muestra que la línea ajustada se ajusta adecuadamente a los datos.
R-cuad. para la línea ajustada
El valor de R-cuad. (R2) para la línea de regresión ajustada indica el porcentaje de la variación en las respuestas de probabilidad de aceptación que es explicado por el modelo de regresión.
Interpretación
R2 varía de 0 a 100%. Por lo general, mientas mayor sea el valor de R2, mejor se ajustará el modelo a los datos. Los valores de R2 superiores a 90% normalmente indican un ajuste de los datos muy adecuado.

Para este ejemplo, el R-cuad. es 0.969376. La línea ajustada se ajusta muy bien a los datos y el modelo explica casi el 97% de la varianza.
T
T es el estadístico t para la hipótesis alternativa de que el sesgo ≠ 0.
La prueba t compara este estadístico t observado con un valor crítico en la distribución t con (n-1) grados de libertad para determinar si el sesgo del sistema de medición es estadísticamente significativo.
GL
El valor de grados de libertad (GL) se utiliza para determinar el valor p. Para el método AIAG, GL = número de ensayos –1. Para el método de regresión, GL es el número de puntos utilizados para crear la línea ajustada –2.
Valor p
Para determinar si el sesgo en el sistema de medición es estadísticamente significativo, compare el valor p con el nivel de significancia. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe sesgo cuando no hay ningún sesgo significativo.
Interpretación
Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula. Si el valor p es menor que el valor del nivel de signficancia (α), usted puede rechazar la hipótesis nula de que el sesgo del sistema de medición es igual a 0.
Curva de rendimiento del sistema de medición
La curva de rendimiento del sistema de medición indica la probabilidad estimada de aceptación en función del valor de referencia para el elemento. La línea de referencia vertical indica los límites que usted ingresó para el análisis.
Interpretación
Si usted especifica un límite inferior de tolerancia, los valores de referencia y las probabilidades de aceptación mostrarán una tendencia ascendente. Si usted especifica un límite superior de tolerancia, como el incremento de los valores de referencia, las probabilidades de aceptación disminuirán.
Si un sistema de medición tiene un límite superior e inferior y se puede presuponer linealidad y uniformidad del error, usted puede mostrar límites de tolerancia superior e inferior en la curva de rendimiento del sistema de medición. La curva aparece como una imagen de espejo.
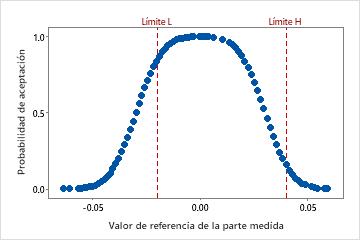
Para estos datos, la probabilidad de aceptar un elemento en el límite inferior de tolerancia (límite L) de −0.020 es alta. La probabilidad de aceptación aumenta a medida que aumentan los valores de referencia hasta el valor de referencia de 0.01. Entonces la probabilidad de aceptación disminuye. La probabilidad de aceptación en el límite superior de tolerancia (límite H) es una probabilidad de aproximadamente 0.15.
