En este tema
Coeficiente de concordancia de Kendall
Utilice el estadístico de Kendall con datos ordinales de tres o más niveles.
En la descripción del método, sin pérdida de generalidad, se presupone que cada evaluador clasifica cada sujeto una sola vez y que hay k evaluadores por cada sujeto. Entonces, para calcular el coeficiente de Kendall, los k evaluadores representan los k ensayos realizados por cada evaluador.
Supongamos que los datos están organizados en una tabla k x N con cada fila representando las jerarquías asignadas por un evaluador en particular a los N sujetos.
Fórmulas
Cuando no se conoce el valor estándar real, Minitab estima el coeficiente de Kendall mediante:
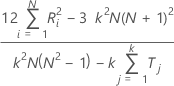
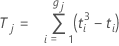
Notación
| Término | Description |
|---|---|
| N | el número de sujetos |
| Σ Ri2 | la suma de las sumas al cuadrado de las jerarquías para cada uno de los N sujetos jerarquizados |
| K | el número de evaluadores |
| Tj | Tj asigna el promedio de las clasificaciones a la observación empatada |
| Término | Description |
|---|---|
| ti | el número de jerarquías empatadas en la agrupación iésima de empates |
| gj | el número de grupos de empates en el conjunto jésimo de jerarquías |
Probar la significancia del coeficiente de concordancia de Kendall
Para probar la significancia del coeficiente de Kendall, utilice:
c 2= k (N – 1) W
Notación
| Término | Description |
|---|---|
| c 2 | está distribuido como chi-cuadrada con N – 1 grados de libertad |
| k | el número de evaluadores |
| N | el número de sujetos |
| W | el coeficiente calculado de Kendall |
Coeficiente de correlación de Kendall
Utilice el estadístico de Kendall con datos ordinales de tres o más niveles.
En la descripción del método, sin pérdida de generalidad, se presupone que cada evaluador clasifica cada sujeto una sola vez y que hay k evaluadores por cada sujeto. Entonces, para calcular el coeficiente de correlación de Kendall, los k evaluadores representan los k ensayos realizados por los evaluadores.
Cuando se conoce el valor estándar verdadero, Minitab estima el coeficiente de correlación de Kendall calculando el promedio de los coeficientes de Kendall entre cada evaluador y el estándar.
El coeficiente de correlación de Kendall para la concordancia de los ensayos con el valor estándar conocido es el promedio de los coeficientes de correlación de Kendall de los diferentes ensayos.
Fórmulas
Minitab calcula el coeficiente de Kendall entre cada ensayo y el valor estándar usando:

Notación
| Término | Description |
|---|---|
| TX | número de pares empatados en X = 0.5 Σi ni+ (ni+– 1) |
| TY | número de pares empatados en Y = 0.5 Σj n+j (n+j– 1) |
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| Término | Description |
|---|---|
| ni+ | número de observaciones en la fila iésima |
| n+j | número de observaciones en la columna jésima |
| nij | observaciones en la celda correspondiente a la fila iésima y la columna jésima |
| nkl | observaciones en la celda correspondiente a la fila késima y la columna lésima |
| n++ | número total de observaciones |
Referencia
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Probar la significancia del coeficiente de correlación de Kendall
Fórmula
Para probar la significancia del coeficiente de Kendall cuando se conoce el valor estándar real, utilice:
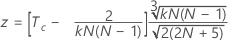
utilice:
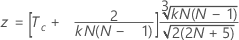
Notación
| Término | Description |
|---|---|
| Tc | el promedio de los coeficientes de correlación de Kendall entre cada evaluador y el valor estándar |
| N | el número total de sujetos |
| k | el número de evaluadores |
