Si los datos exhiben dispersión excesiva o dispersión insuficiente, una gráfica de atributos de Laney (una Gráfica P′ de Laney o una Gráfica U′ de Laney) puede distinguir con mayor exactitud entre la variación por causas comunes y la variación por causas especiales que una gráfica de atributos tradicional (por ejemplo, una Gráfica P o una Gráfica U). Los cálculos para las gráficas de atributos de Laney incluyen Sigma Z, que es un ajuste para la dispersión excesiva o insuficiente. Un valor Sigma Z de 1 indica que no es necesario ningún ajuste y que la gráfica de atributos de Laney es exactamente lo mismo que una gráfica de atributos tradicional.
Para crear una gráfica P' de Laney, elija . Para crear una gráfica U' de Laney, elija .
¿Qué es dispersión excesiva?
La dispersión excesiva existe cuando los datos presentan más variación de la que podría esperarse con base en una distribución binomial (para defectuosos) o una distribución de Poisson (para defectos). Las gráficas P y U tradicionales presuponen que su tasa de defectuosos o defectos permanece constante en el tiempo. Sin embargo, factores de ruido externos, que no son causas especiales, por lo general causan cierta variación en la tasa de defectuosos o defectos en el tiempo.
Los límites de control en una gráfica P o U tradicional se hacen más estrechos cuando los subgrupos son más grandes. Si los subgrupos son lo suficientemente grandes, la dispersión excesiva puede hacer que los puntos parezcan estar fuera de control cuando no lo están. Para una gráfica de atributos de Laney, la definición de variación por causas comunes no solo incluye la variación dentro de los subgrupos, sino también la variación promedio entre los subgrupos consecutivos. Si existe dispersión excesiva, los límites de control en una gráfica de atributos de Laney son más amplios que los de una gráfica de atributos tradicional.
La relación entre el tamaño del subgrupo y los límites de control en una gráfica de control de atributos tradicional es similar a la que existe entre la potencia y una prueba t para 1 muestra. Con muestras más grandes, la prueba t tiene más potencia para detectar una diferencia. Sin embargo, si la muestra es lo suficientemente grande, incluso una diferencia muy pequeña que no sea de interés se puede tornar significativa. Por ejemplo, con una muestra de 1,000,000 de observaciones, una prueba t puede determinar que una media de 50.001 para la muestra es significativamente diferente de 50. Sin embargo, una diferencia de 0.001 puede que no tenga repercusiones prácticas para el proceso.
¿Qué es dispersión insuficiente?
La dispersión insuficiente es lo opuesto a la dispersión excesiva. La dispersión insuficiente existe cuando los datos presentan menos variación de la que se esperaría con base en una distribución binomial (para defectuosos) o una distribución de Poisson (para defectos). La dispersión insuficiente puede ocurrir cuando los subgrupos adyacentes están correlacionados entre sí, lo que también se conoce como autocorrelación.
Cuando los datos exhiben dispersión insuficiente, los límites de control de una gráfica P o U tradicional pueden ser demasiado amplios. Si los límites de control son demasiado amplios, usted podría pasar por alto la variación por causas especiales y confundirla con una variación por causas comunes. Si existe dispersión insuficiente, los límites de control de una gráfica de atributos de Laney son más estrechos que los de una gráfica de atributos tradicional.
Por ejemplo, a medida que una herramienta se desgasta, el número de defectos puede aumentar. El aumento en los conteos de defectos en los diferentes subgrupos puede hacer que los subgrupos sean más similares de lo que serían en virtud de las probabilidades.
Comparación de las gráficas de atributos tradicionales con las gráficas de atributos de Laney
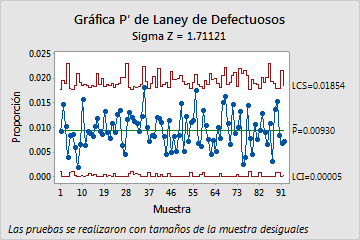
Las siguientes gráficas muestran una gráfica P tradicional y una gráfica P' de Laney de los mismos datos. Estos datos también aparecen en el ejemplo de la Gráfica P' de Laney y el ejemplo del Diagnóstico de gráfica P. Los subgrupos son muy grandes, con un promedio de alrededor de 2500 observaciones en cada uno. Además, la prueba de Diagnóstico de gráfica P revela dispersión excesiva en los datos.
Los tamaños grandes de los subgrupos producen límites de control estrechos en la gráfica P tradicional. Con los límites de control estrechos, la dispersión excesiva hace que varios de los subgrupos parezcan estar fuera de control. Sin embargo, la gráfica P' de Laney muestra que el proceso realmente está bajo control. Ninguno de los puntos se encuentra fuera de los límites de control.
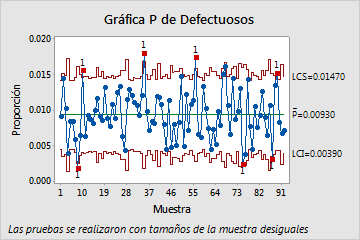
Gráfica P tradicional