Sigma (σ) es la desviación estándar del proceso. Si usted ingresa un valor histórico para σ, Minitab utiliza ese valor histórico. De lo contrario, Minitab emplea uno de los siguientes métodos para estimar σ a partir de los datos.
Método Rbarra
Minitab utiliza el rango de cada subgrupo,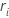 
, para calcular 
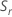, que es un estimador sin sesgo de σ:
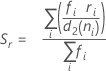
donde
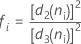
Cuando el tamaño del subgrupo es constante, la fórmula se simplifica a lo siguiente:
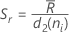
donde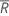 
(Rbarra) es la media de los rangos de los subgrupos, calculada de la siguiente manera:
Notación
| Término | Description |
|---|---|
| ri | rango del subgrupo i |
| m | número de subgrupos |
| d2(·) | valor de la constante de eliminación de sesgo d2 que corresponde al valor especificado entre paréntesis. |
| ni | número de observaciones del subgrupo i |
| d3(·) | valor de la constante de eliminación de sesgo d3 que corresponde al valor especificado entre paréntesis. |
Método de desviación estándar agrupada
La desviación estándar agrupada (Sp) viene dada por la siguiente fórmula:
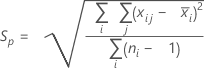
Cuando el tamaño de los subgrupos es constante, la Sp también se puede calcular de la siguiente manera:
Con constante de eliminación de sesgo
Por opción predeterminada, Minitab aplica la constante de eliminaicón de sesgo, c4(), cuando usted utiliza la desviación estándar agrupada para estimar σ:
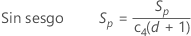
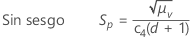
Notación
| Término | Description |
|---|---|
| xij | jésima observación del iésimo subgrupo |
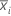 | media del subgrupo i |
| ni | número de observaciones del subgrupo i |
| μv | media de las varianzas de los subgrupos |
| c4(·) | valor de la constante de eliminación de sesgo c4 que corresponde al valor que se especifica entre paréntesis. |
| d | grados de libertad para Sp, que vienen dados por la siguiente fórmula:
 |
