La desviación estándar del proceso también se conoce como sigma, o σ. Si usted ingresa un valor histórico para sigma, Minitab utiliza ese valor histórico. De lo contrario, Minitab emplea uno de los siguientes métodos para estimar el valor de sigma a partir de los datos.
En este tema
Método Rbarra
Minitab utiliza el rango de cada subgrupo, 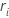 , para calcular
, para calcular 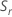 , que es un estimador sin sesgo de σ:
, que es un estimador sin sesgo de σ:
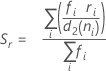
donde
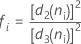
Cuando el tamaño del subgrupo es constante, la fórmula se simplifica a lo siguiente:
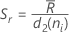
donde 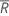 (Rbarra) es la media de los rangos de los subgrupos, calculada de la siguiente manera:
(Rbarra) es la media de los rangos de los subgrupos, calculada de la siguiente manera:

Notación
| Término | Description |
|---|---|
| ri | rango del subgrupo i |
| m | número de subgrupos |
| d2(·) | valor de la constante de eliminación de sesgo d2 que corresponde al valor especificado entre paréntesis. |
| ni | número de observaciones del subgrupo i |
| d3(·) | valor de la constante de eliminación de sesgo d3 que corresponde al valor especificado entre paréntesis. |
Método Sbarra
Sin constante de eliminación de sesgo
Si usted no utiliza una constante de eliminación de sesgo, entonces Sbarra es la media de las desviaciones estándar de los subgrupos:
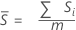
Con constante de eliminación de sesgo
Si utiliza la constante de eliminación de sesgo, c4(ni), entonces Sbarra se calcula de la siguiente manera:
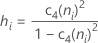
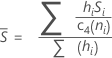
Cuando el tamaño del subgrupo es constante, Sbarra es:
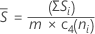
Notación
| Término | Description |
|---|---|
| c4 (ni) | valor de la constante de eliminación de sesgo c4 que corresponde al valor que se especifica entre paréntesis. |
| Si | desviación estándar del subgrupo i |
| m | número de subgrupos |
Método de desviación estándar agrupada
La desviación estándar agrupada (Sp) viene dada por la siguiente fórmula:
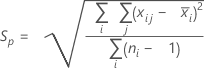
Cuando el tamaño de los subgrupos es constante, la Sp también se puede calcular de la siguiente manera:

Con constante de eliminación de sesgo
Por opción predeterminada, Minitab aplica la constante de eliminaicón de sesgo, c4(), cuando usted utiliza la desviación estándar agrupada para estimar σ:
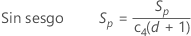
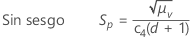
Notación
| Término | Description |
|---|---|
| xij | jésima observación del iésimo subgrupo |
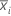 | media del subgrupo i |
| ni | número de observaciones del subgrupo i |
| μv | media de las varianzas de los subgrupos |
| c4(·) | valor de la constante de eliminación de sesgo c4 que corresponde al valor que se especifica entre paréntesis. |
| d | grados de libertad para Sp, que vienen dados por la siguiente fórmula:
 |
Constantes de eliminación de sesgo d2(), d3() y d4()
d2(N) es el valor esperado del rango de N observaciones de una población normal con desviación estándar = 1. Por lo tanto, si r es el rango de una muestra de N observaciones de una distribución normal con desviación estándar = σ, entonces E(r) = d2(N)σ.
d3(N) es la desviación estándar del rango de N observaciones de una población normal con σ = 1. Por lo tanto, si r es el rango de una muestra de N observaciones de una distribución normal con una desviación estándar = σ, entonces desv.est.(r) = d3(N)σ.
Utilice la siguiente tabla para hallar una constante de eliminación de sesgo para un valor dado, N. (Para determinar el valor de N, consulte la fórmula del estadístico de interés.)

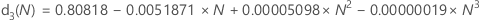
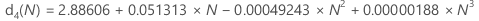
- D. J. Wheeler y D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1.128 | 0.8525 | 0.954 |
| 3 | 1.693 | 0.8884 | 1.588 |
| 4 | 2.059 | 0.8798 | 1.978 |
| 5 | 2.326 | 0.8641 | 2.257 |
| 6 | 2.534 | 0.8480 | 2.472 |
| 7 | 2.704 | 0.8332 | 2.645 |
| 8 | 2.847 | 0.8198 | 2.791 |
| 9 | 2.970 | 0.8078 | 2.915 |
| 10 | 3.078 | 0.7971 | 3.024 |
| 11 | 3.173 | 0.7873 | 3.121 |
| 12 | 3.258 | 0.7785 | 3.207 |
| 13 | 3.336 | 0.7704 | 3.285 |
| 14 | 3.407 | 0.7630 | 3.356 |
| 15 | 3.472 | 0.7562 | 3.422 |
| 16 | 3.532 | 0.7499 | 3.482 |
| 17 | 3.588 | 0.7441 | 3.538 |
| 18 | 3.640 | 0.7386 | 3.591 |
| 19 | 3.689 | 0.7335 | 3.640 |
| 20 | 3.735 | 0.7287 | 3.686 |
| 21 | 3.778 | 0.7242 | 3.730 |
| 22 | 3.819 | 0.7199 | 3.771 |
| 23 | 3.858 | 0.7159 | 3.811 |
| 24 | 3.895 | 0.7121 | 3.847 |
| 25 | 3.931 | 0.7084 | 3.883 |
| N | d2(N) |
|---|---|
| 26 | 3.964 |
| 27 | 3.997 |
| 28 | 4.027 |
| 29 | 4.057 |
| 30 | 4.086 |
| 31 | 4.113 |
| 32 | 4.139 |
| 33 | 4.165 |
| 34 | 4.189 |
| 35 | 4.213 |
| 36 | 4.236 |
| 37 | 4.259 |
| 38 | 4.280 |
| 39 | 4.301 |
| 40 | 4.322 |
| 41 | 4.341 |
| 42 | 4.361 |
| 43 | 4.379 |
| 44 | 4.398 |
| 45 | 4.415 |
| 46 | 4.433 |
| 47 | 4.450 |
| 48 | 4.466 |
| 49 | 4.482 |
| 50 | 4.498 |
Constantes de eliminación de sesgo c4() y c5()
c4()

c5()

Notación
| Término | Description |
|---|---|
| Γ() | función gamma |
