Métodos y fórmulas para Gráfica G

Seleccione el método o la fórmula de su preferencia.

En este tema

Puntos graficados
Línea central y límites de control
Pruebas para detectar causas especiales, incluida la prueba de Benneyan

Puntos graficados

Si sus datos se registran como la fecha de cada evento, cada punto graficado, x_i, representa el número de días entre eventos sucesivos. Si sus datos se registran como el número de oportunidades entre eventos, cada punto graficado representa el número de oportunidades entre eventos sucesivos.

Línea central y límites de control

Línea central (LC)

La línea central es el percentil 50 de la distribución. La línea central es igual a G2 – 1.

Nota

Se resta 1 porque Minitab utiliza la definición de "número hasta" de la distribución geométrica en sus cálculos, pero grafica los valores de "número entre" en la gráfica G.

G2 es igual a INVCDF (0.5) para una distribución geométrica con parámetro p.

Minitab proporciona 2 valores, G2_a y G2_b (G2_a = G2_b – 1), con 2 probabilidades p2_a y p2_b (p2_a < p2_b). Mediante una interpolación lineal simple, G2 = G2_a + (0.5 – p2_a) / (p2_b – p2_a).

Límite de control inferior (LCI)

LCI = G1 – 1

G1 es igual a INVCDF (0.00135) para una distribución geométrica con parámetro p.

Minitab proporciona 2 valores, G1_a y G1_b (G1_a = G1_b – 1), con 2 probabilidades p1_a y p1_b (p1_a < p1_b). Mediante una interpolación lineal simple, G1 = G1_a + (.00135 – p1_a) / (p1_b – p1_a).

Límite de control superior (LCS)

LCS = G3 – 1

G3 es igual a INVCDF (0,99865) para una distribución geométrica con parámetro p.

Minitab proporciona 2 valores, G3_a y G3_b (G3_a = G3_b – 1), con 2 probabilidades p3_a y p3_b (p3_a < p3_b). Mediante una interpolación lineal simple, obtenemos G3 = G3_a + (0,99865 – p3_a) / (p3_b – p3_a).

Notación

Término	Description
N	número de valores de datos utilizados en los cálculos (Si los datos son fechas, reste 1 porque Minitab grafica las diferencias.)
	promedio de los puntos graficados
Probabilidad de evento (p)

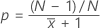Pruebas para detectar causas especiales, incluida la prueba de Benneyan

Pruebas 1−4

La Prueba 1 se basa en la distribución geométrica. Las pruebas 2, 3 y 4 son idénticas a las pruebas utilizadas en las gráficas de atributos.

Si K = 3, los valores de G1 y G3 utilizados para los límites de control definen los fracasos de la Prueba 1. Si K es menor o mayor que 3, los puntos graficados por debajo de G1' no pasan la Prueba 1 y los puntos graficados por encima de G3' no pasan la Prueba 1.

G1 = INVCDF (0.00135) para una distribución geométrica con parámetro p.
G3 = INVCDF (0.99865) para una distribución geométrica con parámetro p; promedio de los puntos graficados
G1' = INVCDF (p1') para una distribución geométrica con parámetro p
G3' = INVCDF (p2') para una distribución geométrica con parámetro p
p1' = CDF (–K) para una distribución normal con media = 0 y desviación estándar = 1
p2' = CDF (K) para una distribución normal con media = 0 y desviación estándar = 1

Prueba de Benneyan

La prueba de Benneyan cuenta el número de puntos graficados consecutivos iguales al límite de control inferior utilizando la siguiente fórmula para generar una señal:

Minitab redondea cp al entero más cercano y utiliza ese valor como el número de puntos consecutivos iguales al límite de control inferior que se requieren para producir una señal.

Consulte Benneyan¹ para obtener más información sobre la prueba de Benneyan.

Notación

Término	Description
CDF()	CDF para una distribución normal con media 0 y desviación estándar 1
k	parámetro para la prueba 1. El valor predeterminado es 3.

¹ J. C. Benneyan (2001). "Performance of Number-Between g-Type Statistical Control Charts for Monitoring Adverse Events", Health Care Management Science, 4, 319−336.