En este tema
Puntos graficados
Los puntos graficados en la gráfica G representan el número de oportunidades entre eventos o los días entre eventos.
Interpretación
Si el proceso está bajo control, los puntos variarán de manera aleatoria alrededor de la línea central y el proceso presentará solo variación por causas comunes. Investigue los puntos que no pasen cualquiera de las pruebas para detectar causas especiales o que presentan patrones no aleatorios de posible variación por causas especiales.
Línea central
La línea central en la gráfica G es el percentil 50 de la distribución.
Interpretación
Utilice la línea central para observar cómo funciona el proceso en comparación con el promedio. Si el proceso está bajo control, entonces los puntos varían de manera aleatoria alrededor de la línea central.
Precaución
No confunda la línea central con el valor objetivo del proceso. El objetivo es el resultado deseado. La línea central es el resultado real.
Límites de control
Los límites de control son las líneas horizontales que se encuentran por encima y por debajo de la línea central. En una gráfica G, el límite de control inferior siempre se establece en 0. El límite de control superior indica si un proceso está fuera de control y se basan en la CDF inversa de la distribución geométrica.
Pruebas para detectar causas especiales
Las pruebas para detectar causas especiales evalúan si los puntos graficados están distribuidos aleatoriamente dentro de los límites de control.
Interpretación
Utilice las pruebas para detectar causas especiales para determinar qué observaciones puede tener que investigar y para identificar patrones y tendencias en los datos. Cada una de estas pruebas para detectar causas especiales detecta un patrón o una tendencia específicos en los datos, lo que revela un aspecto diferente de la inestabilidad del proceso. Por ejemplo, la Prueba 1 detecta un solo punto fuera de control. La prueba 2 detecta un posible cambio rápido en el proceso.
Cuatro pruebas están disponibles con esta gráfica de control.
- Prueba 1: Un punto a más de 3σ de la línea central
- La Prueba 1 identifica subgrupos que son poco comunes en comparación con otros subgrupos. La prueba 1 se reconoce universalmente como una prueba necesaria para detectar situaciones fuera de control. Si pequeños cambios rápidos en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
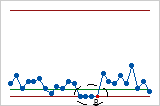
- Prueba de Benneyan: Puntos sucesivos iguales a 0
- La prueba de Benneyan cuenta el número de puntos graficados consecutivos que son iguales a 0. Cuando un punto en una gráfica G no pasa la prueba de Benneyan, el punto se denota con una B. El número de puntos que se requieren para señalar la prueba de Benneyan es una función de la tasa deseada de falsas alarmas y de la probabilidad del evento. La tasa de falsas alarmas se basa en la probabilidad que se asocia con el argumento de la Prueba 1, que es 3 por opción predeterminada.
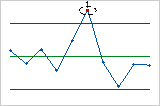
- Prueba 2: Nueve puntos consecutivos en el mismo lado de la línea central
- La prueba 2 identifica cambios rápidos en la variación del proceso. Si pequeños cambios rápidos en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
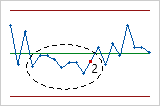
- Prueba 3: Seis puntos consecutivos, todos en orden creciente o decreciente
- La Prueba 3 detecta tendencias. Esta prueba busca series largas de puntos consecutivos que de manera constante aumentan o disminuyen de valor.
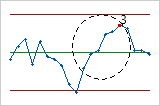
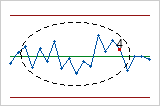
- Prueba 4: Catorce puntos consecutivos, alternativamente arriba y abajo
- La Prueba 4 detecta variación sistemática. Usted desea que el patrón de variación en un proceso sea aleatorio, pero un punto que no pasa la Prueba 4 podría indicar que el patrón de variación es predecible.
Etapas
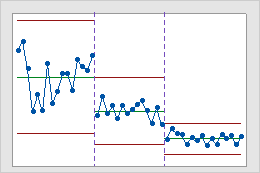
Utilice etapas para crear una gráfica de control histórica que muestre cómo cambia un proceso durante períodos de tiempo específicos. Por opción predeterminada, Minitab vuelve a calcular la línea central y los límites de control de cada etapa. Para obtener más información, vaya a Agregar etapas para mostrar cómo cambió un proceso.
Interpretación
Esta gráfica de control histórica muestra tres etapas de un proceso, las cuales representan el antes, durante y después de la implementación de un nuevo procedimiento.