En este tema
Puntos graficados
Los puntos graficados en una gráfica Tcuadrada son los valores T2 de cada grupo. Los puntos graficados en una gráfica de varianza generalizada son los estadísticos de varianza generalizada de cada subgrupo.
Interpretación
Si el proceso está bajo control, los puntos se ubicarán por debajo del límite de control superior y el proceso presentará solo variación por causas comunes. Investigue los puntos que se ubiquen por encima del límite de control superior. Una desventaja de las gráficas multivariadas es que la escala no está relacionada con la escala de ninguna de las variables y las señales de fuera de control no revelan cuál variable (o combinación de variables) causó la señal.
Línea central
La línea central en una gráfica Tcuadrada es la mediana de la distribución teórica de los estadísticos T2. La línea central en la gráfica de varianza generalizada es la determinante de la matriz de covarianzas de la muestra
Interpretación
Utilice la línea central para observar cómo funciona el proceso en comparación con el promedio. Si el proceso está bajo control, entonces los puntos varían de manera aleatoria alrededor de la línea central.
Límites de control
Los límites de control son las líneas horizontales que se encuentran por encima y por debajo de la línea central. Los límites de control indican si un proceso está fuera de control y se basan en la variación observada dentro de los subgrupos y en la variación esperada en los puntos graficados. La gráfica Tcuadrada solo tiene un límite de control superior. La gráfica de varianza generalizada tiene límites de control tanto superior como inferior.
Valores descompuestos de T2
Los valores descompuestos de T2 proporcionan la contribución individual de cada variable para todos los puntos fuera de control en una gráfica T2.
En una gráfica T2, los puntos individuales son valores compuestos que representan variables múltiples. Por lo que una gráfica T2 no muestra cuánto contribuye cualquier variable con el valor del punto combinado, lo que complica la interpretación de los puntos que están fuera de control. Cuando un punto está fuera de control en una gráfica T2, usted no puede determinar si todas las variables, algunas de las variables o solo una de las variables contribuyó a la condición de fuera de control. Sin embargo, los valores descompuestos de T2 indican si una variable contribuyó más a la condición de fuera de control que las demás variables.
Matrices de covarianzas
Una matriz de covarianzas es una matriz cuadrada que contiene las varianzas y covarianzas de diferentes variables. Los elementos de la diagonal de la matriz contienen las varianzas de las variables, mientras que los elementos que se encuentran fuera de la diagonal contienen las covarianzas entre todos los pares posibles de variables.
La matriz de varianzas y covarianzas es simétrica, porque la covarianza entre X y Y es igual a la covarianza entre Y y X. Por lo tanto, la covarianza para cada par de variables aparece dos veces en la matriz: la covarianza entre las variables iésima y jésima se muestra en las posiciones (i, j) y (j, i).
Después de almacenar las matrices de covarianzas, elija para ver las matrices de covarianzas.
Interpretación
| X | Y | Z | |
| X | 2,0 | −0,86 | −0,15 |
| Y | −0,86 | 3,4 | 0,48 |
| Z | −0,15 | 0,48 | 0,82 |
Las varianzas se muestran en negrita a lo largo de la diagonal. Las varianzas de X, Y y Z son 2.0, 3.4 y 0.82, respectivamente. La covarianza entre X y Y es −0.86, la covarianza entre X y Z es −0.15 y la covarianza entre Y y Z es 0.48.
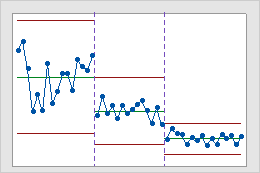
Etapas
Utilice etapas para crear una gráfica de control histórica que muestre cómo cambia un proceso durante períodos de tiempo específicos. Por opción predeterminada, Minitab vuelve a calcular la línea central y los límites de control de cada etapa. Para obtener más información, vaya a Agregar etapas para mostrar cómo cambió un proceso.
Interpretación
Esta gráfica de control histórica muestra tres etapas de un proceso, las cuales representan el antes, durante y después de la implementación de un nuevo procedimiento.