En este tema
Puntos graficados
Cada punto en una gráfica P' de Laney representa la proporción de unidades o elementos defectuosos en un subgrupo.
Interpretación
Si el proceso está bajo control, los puntos varían de manera aleatoria alrededor de la línea central y el proceso solo exhibe variación por causas comunes. Investigue los puntos que se encuentran fuera de los límites de control o que exhiben patrones no aleatorios de posible variación por causas especiales.
Línea central
La línea central en una gráfica P' de Laney representa la proporción promedio de unidades defectuosas en el proceso. La proporción promedio de unidades defectuosas también se conoce como la proporción del proceso.
Interpretación
Utilice la línea central para observar cómo funciona el proceso en comparación con el promedio. Si el proceso está bajo control, entonces los puntos varían de manera aleatoria alrededor de la línea central.
Precaución
No confunda la línea central con el valor objetivo del proceso. El objetivo es el resultado deseado. La línea central es el resultado real.
Límites de control
Precaución
No confunda los límites de control con los límites de especificación. Los límites de especificación representan los requisitos del cliente e indican la cantidad de variación que usted desea ver en el proceso. Los límites de control representan la cantidad real de variación que hay en los datos de la muestra. Un proceso puede estar bajo control y aún así puede no ser capaz de satisfacer las especificaciones.
Sigma Z
Sigma Z mide la dispersión excesiva o la dispersión insuficiente en los datos.
Interpretación
- Un valor Sigma Z de 1 indica que no se requiere ajuste. En este caso, los límites de control en la gráfica P' de Laney son exactamente iguales a los límites de control en una gráfica P tradicional.
- Un valor Sigma Z mayor que 1 indica que los límites de control en la gráfica P' de Laney son más amplios que los límites de control en una gráfica P tradicional para ajustar para la dispersión excesiva.
- Un valor Sigma Z menor que 1 indica que los límites de control en la gráfica P' de Laney son más estrechos que los límites de control en una gráfica P tradicional para ajustar para la dispersión insuficiente.
Por ejemplo, las siguientes gráficas muestran una gráfica P tradicional y una gráfica P' de Laney de los mismos datos. Los subgrupos son grandes y los datos presentan dispersión excesiva.
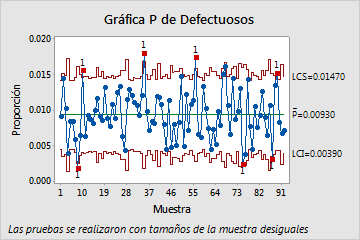
- Gráfica P tradicional
- En la gráfica P tradicional, los tamaños de subgrupo grandes dan como resultado límites de control estrechos. Los límites de control estrechos y la dispersión excesiva hacen que varios de los subgrupos parezcan estar fuera de control.
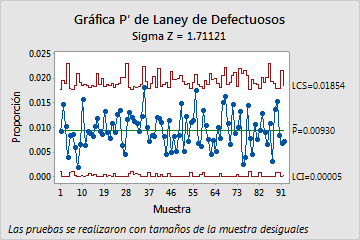
- Gráfica P' de Laney
- Los límites de control en la gráfica P' de Laney se ajustan para la dispersión excesiva. La gráfica P' de Laney muestra que el proceso realmente está bajo control. Ninguno de los puntos se encuentra fuera de los límites de control.
Pruebas para detectar causas especiales
Las pruebas para detectar causas especiales evalúan si los puntos graficados están distribuidos aleatoriamente dentro de los límites de control.
Interpretación
Utilice las pruebas para detectar causas especiales para determinar qué observaciones puede tener que investigar y para identificar patrones y tendencias en los datos. Cada una de estas pruebas para detectar causas especiales detecta un patrón o una tendencia específicos en los datos, lo que revela un aspecto diferente de la inestabilidad del proceso. Por ejemplo, la Prueba 1 detecta un solo punto fuera de control. La prueba 2 detecta un posible cambio rápido en el proceso.
Cuatro pruebas están disponibles con esta gráfica de control.
- Prueba 1: Un punto a más de 3σ de la línea central
- La Prueba 1 identifica subgrupos que son poco comunes en comparación con otros subgrupos. La prueba 1 se reconoce universalmente como una prueba necesaria para detectar situaciones fuera de control. Si pequeños cambios rápidos en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
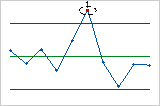
- Prueba 2: Nueve puntos consecutivos en el mismo lado de la línea central
- La prueba 2 identifica cambios rápidos en la proporción de defectuosos del proceso. Si pequeños cambios rápidos en el proceso son de interés, usted puede utilizar la Prueba 2 para complementar la Prueba 1 a fin de crear una gráfica de control que tenga mayor sensibilidad.
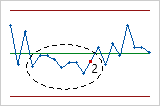
- Prueba 3: Seis puntos consecutivos, todos en orden creciente o decreciente
- La Prueba 3 detecta tendencias. Esta prueba busca series largas de puntos consecutivos que de manera constante aumentan o disminuyen de valor.
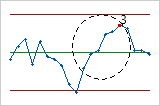
- Prueba 4: Catorce puntos consecutivos, alternativamente arriba y abajo
- La Prueba 4 detecta variación sistemática. Usted desea que el patrón de variación en un proceso sea aleatorio, pero un punto que no pasa la Prueba 4 podría indicar que el patrón de variación es predecible.
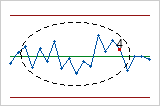
Etapas
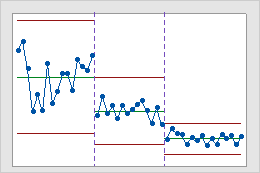
Utilice etapas para crear una gráfica de control histórica que muestre cómo cambia un proceso durante períodos de tiempo específicos. Por opción predeterminada, Minitab vuelve a calcular la línea central y los límites de control de cada etapa. Para obtener más información, vaya a Agregar etapas para mostrar cómo cambió un proceso.
Interpretación
Esta gráfica de control histórica muestra tres etapas de un proceso, las cuales representan el antes, durante y después de la implementación de un nuevo procedimiento.