Cálculo de la desviación estándar
El análisis de capacidad de subgrupos/corto plazo se basa en las cuatro desviaciones estándar siguientes:
Desviación estándar dentro de los subgrupos
σcorto plazo es una estimación de la variación dentro de los subgrupos (por ejemplo, un turno, un operador o un lote de material). Minitab estima la σcorto plazo utilizando uno de los siguientes métodos:
- Desviación estándar agrupada:

donde:
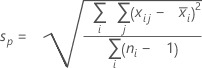
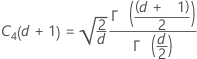
Nota
Si cambia el método predeterminado y elige no utilizar la constante de eliminación de sesgo, la σcorto plazo se estima mediante Sp.
Término Description d Grados de libertad de Sp= Σ (ni- 1) Xij jésima observación del iésimo subgrupo X̅i Media del iésimo subgrupo ni Número de observaciones en el iésimo subgrupo C4(d+1) Constante de eliminación de sesgo Γ(·) Función gamma - Promedio de los rangos de los subgrupos (Rbarra):

donde:
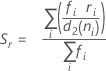
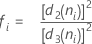
Si todos los valores de n son iguales:
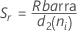
Término Description ri Rango del iésimo subgrupo d2 (ni) Una constante de eliminación de sesgo leída en una tabla (para obtener más información, véase la sección Constantes de eliminación de sesgo d2(), d3() y d4()) d3 (ni) Una constante de eliminación de sesgo leída en una tabla (para obtener más información, véase la sección Constantes de eliminación de sesgo d2(), d3() y d4()) ni Número de observaciones en el iésimo subgrupo - Promedio de las desviaciones estándar de los subgrupos (Sbarra):

donde:
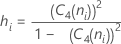
Nota
Si cambia la configuración predeterminada y no utiliza la constante de eliminación de sesgo, la σcorto plazo se estima mediante Σ Si / número de subgrupos.
Término Description C4(ni) Constante de eliminación de sesgo (como se definió para la desviación estándar agrupada) Si Desviación estándar del subgrupo i ni Número de observaciones en el iésimo subgrupo
Deviación estándar entre los subgrupos
La σsubgrupos es una estimación de la variación entre los subgrupos (por ejemplo, subgrupos recopilados a intervalos establecidos, por lotes o por diferentes operadores).

- Promedio del rango móvil:

donde:
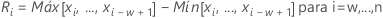
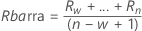
Término Description Ri El iésimo rango móvil w El número de observaciones utilizadas en el rango móvil. El valor predeterminado es w = 2. d2(w) Una constante de eliminación de sesgo leída en una tabla (para obtener más información, véase la sección Constantes de eliminación de sesgo d2(), d3() y d4()) - Mediana del rango móvil:

donde:
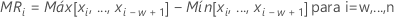
Término Description MRi El iésimo rango móvil 
Mediana del MRi w El número de observaciones utilizadas en el rango móvil. El valor predeterminado es w = 2. d4(w) Una constante de eliminación de sesgo leída en una tabla (para obtener más información, véase la sección Constantes de eliminación de sesgo d2(), d3() y d4()) - Raíz cuadrada de la media de las diferencias sucesivas cuadráticas (MSSD):
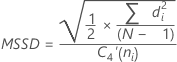
Nota
Si cambia la configuración predeterminada y no utiliza la constante de eliminación de sesgo, la σcorto plazo se estima mediante

Término Description di Diferencias de las medias de grupos sucesivos C4(ni) Constante de eliminación de sesgo (como se definió para la desviación estándar agrupada) C4'(ni) Constante de eliminación de sesgo ≈ c4(ni). Para obtener más información, véase la sección Constante de eliminación de sesgo c4'(). N Número total de observaciones ni Número de observaciones en el iésimo subgrupo
Desviación estándar de subgrupos/corto plazo

| Término | Description |
|---|---|
| σ2Subgrupos | Varianza entre los subgrupos |
| σ2corto plazo | Varianza dentro de los subgrupos |
Desviación estándar general
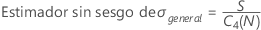
donde:
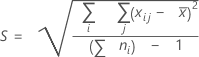
Nota
Por opción predeterminada, Minitab no utiliza la constante de eliminación de sesgo cuando se estima σgeneral. σgeneral se estima mediante S. Si desea estimar la desviación estándar general usando la constate de eliminación de sesgo, puede cambiar esta opción en el cuadro de diálogo secundario Estimaciones cuando realice el análisis de capacidad. Si quiere que Minitab siempre utilice la constante de eliminación de sesgo por opción predeterminada, elija y seleccione las opciones adecuadas.
| Término | Description |
|---|---|
| Xij | La jésima observación en el iésimo subgrupo |
| X̅ | Media del proceso |
| ni | Número de observaciones en el iésimo subgrupo |
| C4 (N) | Constante de eliminación de sesgo (como se definió para la desviación estándar agrupada) |
| N (o Σ ni) | Número total de observaciones |
Transformación de Box-Cox
La transformación de Box-Cox estima un valor de lambda, como se muestra en la siguiente tabla, que minimiza la desviación estándar de una variable transformada estandarizada. La transformación resultante es Yλ cuando λ ҂ 0 y ln Y cuando λ = 0.
El método de Box-Cox busca entre muchos tipos de transformaciones. La siguiente tabla muestra algunas transformaciones comunes donde Y' es la transformación de los datos Y.
| Valor de lambda (λ) | Transformación |
|---|---|
 |
 |
 |
 |
 |
 |
 |
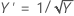 |
 |
 |
