En este tema
- Calidad del lote
- Límite de especificación inferior (LEI) y límite de especificación superior (LES)
- Desviación estándar histórica
- Tamaño del lote
- Nivel de calidad aceptable (AQL) y Nivel de calidad rechazable (RQL o LTPD)
- Riesgo del productor (alfa) y riesgo del consumidor (beta)
- Tamaño de la muestra
- Distancia crítica (valor k)
- Desviación estándar máxima (MSD)
Calidad del lote
- Porcentaje de defectuosos
- Representa el porcentaje de defectuosos como un valor entre 0 y 100. Por ejemplo, si 10 unidades son defectuosas de un tamaño de la muestra de 500, el porcentaje de defectuosos es 2.
- Proporción de defectuosos
- Representa la proporción de defectuosos como un valor entre 0 y 1. Por ejemplo, si 10 unidades son defectuosas de un tamaño de la muestra de 500, la proporción de defectuosos es 0.02.
- Defectuosos por millón
- Representa el nivel de defectuosos como un valor en un millón de unidades. Por ejemplo, 10 defectuosos por millón (DPM) significa que tiene 10 unidades defectuosas por cada millón de unidades.
Límite de especificación inferior (LEI) y límite de especificación superior (LES)
El límite de especificación inferior (LEI) es el mínimo valor permitido para el producto o servicio. Este límite no indica cuál es el desempeño del proceso, pero sí cómo usted desea que sea su desempeño.
El límite de especificación superior (LES) es el máximo valor permitido para el producto o servicio. Este límite no indica cuál es el desempeño del proceso, pero sí cómo usted desea que sea su desempeño.
Debe especificar por lo menos un límite de especificación para un plan de muestreo de aceptación por variables.
Interpretación
Utilice el LEI y el LES para definir los requisitos del cliente y evaluar si su proceso produce elementos que cumplan con los requisitos.
Minitab compara los datos de su proceso con los límites de especificación para determinar si se acepta o rechaza un lote entero de producto.
Desviación estándar histórica
La desviación estándar histórica es la desviación estándar conocida de su proceso. Utilice una desviación estándar histórica cuando haya recolectado suficientes datos en el tiempo para poder determinar con confianza cuál es la desviación estándar del proceso. Si el proceso es estable y está bajo control, entonces puede usar una desviación estándar histórica en lugar de una desviación estándar calculada.
Tamaño del lote
El tamaño del lote es la población de la cual usted recolecta sus muestras cuando decide si aceptará o rechazará el lote entero.
Normalmente, el tamaño de lote se elige para que sea conveniente para envío y manejo tanto para el proveedor como para el consumidor. Por ejemplo, un tamaño de lote conveniente podría ser un envío completo. Debido a que los planes de muestreo presuponen homogeneidad de las partes en un lote, las unidades que conforman un lote se deberían producir en las mismas condiciones del proceso. Además, generalmente es más económico inspeccionar lotes más grandes que una serie de lotes más pequeños.
Nivel de calidad aceptable (AQL) y Nivel de calidad rechazable (RQL o LTPD)
- Nivel de calidad aceptable (AQL)
- El nivel de calidad aceptable (AQL) es la tasa de defectuosos más alta del proceso de un proveedor que se considera aceptable. El AQL describe lo que el plan de muestreo aceptará y el RQL describe lo que el plan de muestreo rechazará. Usted desea designar un plan de muestreo que acepte un lote de producto particular en el AQL la mayoría de las veces.
- Nivel de calidad rechazable (RQL o LTPD)
- El nivel de calidad rechazable (RQL) es la tasa de defectuosos más alta que el consumidor está dispuesto a tolerar en un lote individual. El RQL describe lo que el plan de muestreo rechazará y el AQL describe lo que el plan de muestreo aceptará. Usted desea diseñar un plan de muestreo que rechace un lote de producto particular en el RQL la mayor parte del tiempo.
Interpretación
El consumidor y el proveedor deben acordar la tasa de defectuosos más alta que es aceptable (AQL). El consumidor y el proveedor también deben acordar la tasa de defectuosos más alta que el consumidor tolerará en un lote individual (RQL).
La probabilidad de aceptación en el AQL (100 defectuosos por millón) es de 0.95 y la probabilidad de rechazo es de 0.05. La probabilidad de aceptación en el RQL (300 defectuosos por millón) es de 0.10 y la probabilidad de rechazo es de 0.90.
Método
| Límite de especificación inferior (LEI) | 0.09 |
|---|---|
| Desviación histórica estándar | 0.025 |
| Tamaño del lote | 2500 |
| Nivel de calidad aceptable(AQL) | 100 |
| Riesgo del productor(α) | 0.05 |
| Nivel de calidad rechazable (RQL o LTPD) | 300 |
| Riesgo del consumidor(β) | 0.1 |
Riesgo del productor (alfa) y riesgo del consumidor (beta)
- Riesgo del productor (alfa)
- El riesgo del productor, α, es la probabilidad de rechazar un lote que tiene un nivel de calidad igual al AQL que debería ser aceptado. A medida que aumenta α, aumenta el riesgo de rechazar lotes con tasas de defectuosos iguales al AQL, lo que perjudicaría al productor. El riesgo del productor también se conoce como error tipo I.
- Riesgo del consumidor (beta)
- El riesgo del consumidor, β, es la probabilidad de aceptar un lote con un nivel de calidad igual al RQL que debería ser rechazado. A medida que aumenta β, aumenta el riesgo de aceptar lotes con tasas de defectuosos iguales al RQL, lo que perjudicaría al consumidor. El riesgo del consumidor también se conoce como error tipo II.
Interpretación
Para proteger al productor, el riesgo de rechazar un lote que tenga una calidad aceptable debe ser bajo. Para proteger al consumidor, el riesgo de aceptar un lote que tenga calidad deficiente debe ser bajo.
La probabilidad de aceptación en el AQL es de 0.95 y la probabilidad de rechazo es de 0.05. La probabilidad de aceptación en el RQL es de 0.10 y la probabilidad de rechazo es de 0.90.
Método
| Límite de especificación inferior (LEI) | 0.09 |
|---|---|
| Desviación histórica estándar | 0.025 |
| Tamaño del lote | 2500 |
| Nivel de calidad aceptable(AQL) | 100 |
| Riesgo del productor(α) | 0.05 |
| Nivel de calidad rechazable (RQL o LTPD) | 300 |
| Riesgo del consumidor(β) | 0.1 |
Tamaño de la muestra
En muestreo de aceptación, el tamaño de la muestra es el número de elementos que se seleccionan aleatoriamente de un lote para inspección.
Interpretación
En este ejemplo, el tamaño de la muestra es 104. Debe tomar una muestra de 104 elementos del lote entero del producto.
Planes generados
| Tamaño de la muestra | 104 |
|---|---|
| Distancia crítica (valor k) | 3.55750 |
| Elementos defectuosos en un millón | Probabilidad de aceptación | Probabilidad de rechazo | AOQ | ATI |
|---|---|---|---|---|
| 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 300 | 0.100 | 0.900 | 28.6 | 2261.4 |
Distancia crítica (valor k)
La distancia crítica es el valor que Minitab utiliza para comparar con la media de la muestra y los límites de especificación para determinar si se acepta o rechaza un lote.
Interpretación
Por ejemplo, supongamos que usted toma una muestra de lotes de tubos plásticos. Su plan de muestreo requiere tomar una muestra aleatoria de 104 de los 2500 tubos de un envío. La especificación inferior del grosor de la pared de los tubos es de 0.09 pulgadas. Minitab determina que la distancia crítica será 3.5575.
Si los valores Z son mayores que la distancia crítica y la desviación estándar es menor que la desviación estándar máxima (MSD), entonces acepte todo el lote. En caso contrario, rechácelo.
Planes generados
| Tamaño de la muestra | 104 |
|---|---|
| Distancia crítica (valor k) | 3.55750 |
| Elementos defectuosos en un millón | Probabilidad de aceptación | Probabilidad de rechazo | AOQ | ATI |
|---|---|---|---|---|
| 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 300 | 0.100 | 0.900 | 28.6 | 2261.4 |
Desviación estándar máxima (MSD)
Minitab calcula la desviación estándar máxima (MSD) cuando usted proporciona tanto el LEI como el LES y no proporciona una desviación estándar histórica.
Interpretación
Si los valores Z son mayores que la distancia crítica y la desviación estándar es menor que la desviación estándar máxima (MSD), entonces acepte todo el lote. En caso contrario, rechácelo.
Z.LEI y Z.LES
- Z.LEI = (media – especificación inferior) / desviación estándar
- Z.LES = (especificación superior – media) / desviación estándar
Interpretación
Si los valores Z son mayores que la distancia crítica y la desviación estándar es menor que la desviación estándar máxima (MSD), entonces acepte todo el lote. En caso contrario, rechácelo.
Probabilidad de aceptación y probabilidad de rechazo
La probabilidad de aceptar lotes en el AQL debe estar cerca de 1 – α. La probabilidad de aceptar lotes en el RQL debe estar cerca de β. La probabilidad de rechazar es simplemente 1 – la probabilidad de aceptar.
Interpretación
La probabilidad de aceptación en el AQL (100 defectuosos por millón) es de 0.95 y la probabilidad de rechazo es de 0.05. La probabilidad de aceptación en el RQL (300 defectuosos por millón) es de 0.10 y la probabilidad de rechazo es de 0.90.
Planes generados
| Tamaño de la muestra | 104 |
|---|---|
| Distancia crítica (valor k) | 3.55750 |
| Elementos defectuosos en un millón | Probabilidad de aceptación | Probabilidad de rechazo | AOQ | ATI |
|---|---|---|---|---|
| 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 300 | 0.100 | 0.900 | 28.6 | 2261.4 |
AOQ y AOQL
El nivel de calidad saliente promedio representa la relación entre la calidad del material entrante y la calidad del material saliente, suponiendo que los lotes rechazados se inspeccionarán en un 100% y todos los elementos defectuosos serán reemplazados o reparados.
Nota
Usted debe especificar el tamaño del lote para calcular AOQ y AOQL.
Interpretación
En este ejemplo, cuando el nivel de calidad entrante promedio es 100 defectuosos por millón, la calidad saliente promedio es 91.1 defectuosos por millón. Cuando el nivel de calidad entrante promedio es 300 defectuosos por millón, la calidad saliente promedio es 28.6 defectuosos por millón. La calidad entrante es peor que la calidad saliente debido a que los lotes rechazados se inspeccionarán al 100% y todas las unidades no conformes se reemplazarán o se repararán.
El peor nivel de defectuosos saliente promedio (AOQL) de 104.6 defectuosos por millón ocurre cuando el nivel de calidad entrante es 140.0 defectuosos por millón.
Planes generados
| Tamaño de la muestra | 104 |
|---|---|
| Distancia crítica (valor k) | 3.55750 |
| Elementos defectuosos en un millón | Probabilidad de aceptación | Probabilidad de rechazo | AOQ | ATI |
|---|---|---|---|---|
| 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 300 | 0.100 | 0.900 | 28.6 | 2261.4 |
Límite(s) de calidad saliente promedio (AOQL)
| AOQL | En defectuosos por millón |
|---|---|
| 104.6 | 140.0 |
ATI
Nota
Usted debe especificar el tamaño del lote para calcular la ATI.
Interpretación
En este ejemplo, cuando el nivel de calidad entrante promedio es 100 defectuosos por millón, el número promedio de unidades inspeccionadas por lote es 223.2. Esto se debe a que 95% de las veces usted inspeccionará 104 elementos y aprobará el lote, y 5% de las veces usted rechazará el lote e inspeccionará los 2500 elementos. Cuando el nivel de calidad entrante promedio es 300 defectuosos por millón, el número promedio de unidades inspeccionadas por lote es 2261.4, lo cual por poco alcanza la totalidad del envío.
Planes generados
| Tamaño de la muestra | 104 |
|---|---|
| Distancia crítica (valor k) | 3.55750 |
| Elementos defectuosos en un millón | Probabilidad de aceptación | Probabilidad de rechazo | AOQ | ATI |
|---|---|---|---|---|
| 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 300 | 0.100 | 0.900 | 28.6 | 2261.4 |
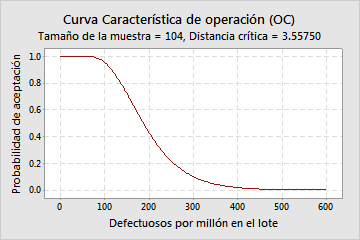
Curva OC
La curva Característica de operación (OC) muestra la capacidad de un plan de muestreo de aceptación para distinguir entre lotes de buena y de mala calidad. La curva OC grafica la probabilidad de aceptar lotes que tienen niveles de calidad entrante diferentes para cada plan de muestreo.
Interpretación
En este ejemplo, si el valor real de defectuosos por millón es 100, usted tiene una probabilidad de 0.950 de aceptar este lote con base en la muestra y una probabilidad de 0.050 de rechazarlo. Si el valor real de defectuosos por millón es 300, tiene una probabilidad de 0.100 de aceptar este lote y una probabilidad de 0.900 de rechazarlo.
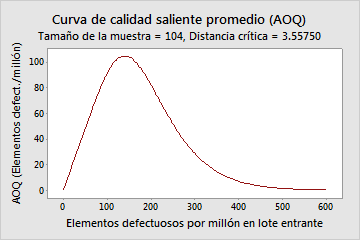
Curva AOQ
La curva de calidad saliente promedio (AOQ) muestra la relación entre la calidad del material entrante y la calidad del material saliente, suponiendo que los lotes rechazados se inspeccionarán en un 100% y los elementos defectuosos se reemplazarán o repararán y se volverán a inspeccionar (inspección de rectificación).
Interpretación
En este ejemplo, cuando el nivel de calidad entrante promedio es 100 defectuosos por millón, la calidad saliente promedio es 91.1 defectuosos por millón. Cuando el nivel de calidad entrante promedio es 300 defectuosos por millón, la calidad saliente promedio es 28.6 defectuosos por millón. La calidad entrante es peor que la calidad saliente debido a que los lotes rechazados se inspeccionarán al 100% y todas las unidades no conformes se reemplazarán o se repararán.
El peor nivel de defectuosos saliente promedio (AOQL) de 104.6 defectuosos por millón ocurre cuando el nivel de calidad entrante es 140.0 defectuosos por millón.
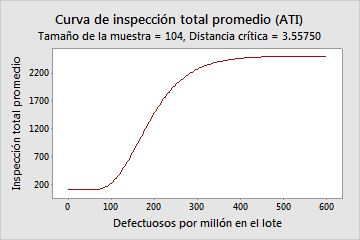
Curva ATI
La curva de inspección total promedio (ATI) muestra la relación entre la calidad del material entrante y el número de elementos que se deben revisar, suponiendo que los lotes rechazados se inspeccionarán en un 100% y los elementos defectuosos se reemplazarán o repararán e inspeccionarán de nuevo (inspección de rectificación).
Interpretación
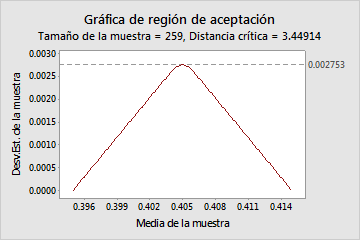
Gráfica de región de aceptación
La gráfica de región de aceptación se utiliza para ilustrar los requisitos de la muestra. Cuando se conocen las especificaciones superior e inferior y se desconoce la desviación estándar, la gráfica de región de aceptación le permite ver la región de las medias de la muestra y las desviaciones estándar de la muestra con las cuales usted aceptará un lote.
Interpretación
A medida que la desviación estándar de la muestra aumenta y alcanza el máximo, la media debe ubicarse en el objetivo para que usted acepte un envío. Si la variación del proceso es aproximada y la desviación estándar es pequeña, la media puede variar entre los límites de especificación.