Ejemplo de creación de un plan de muestreo de aceptación por variables

Un ingeniero de manufactura recibe envíos semanales de segmentos de tubería de plástico de 2 pulgadas para un proceso de ensamblaje. El tamaño del lote es 2500.

El ingeniero decide implementar un plan de muestreo para verificar el grosor de la pared de la tubería. La especificación inferior del grosor de la pared de los tubos es 0,09 pulgadas. El ingeniero y el proveedor convienen en que el AQL es de 100 defectuosos por millón y el RQL es de 300 defectuosos por millón.

Elija Estadísticas > Herramientas de calidad > Muestreo de aceptación por variables > Crear/comparar.
En la lista desplegable, seleccione Crear un plan de muestreo.
En Unidades para niveles de calidad, seleccione Defectuosos por millón.
En Nivel de calidad aceptable (AQL), ingrese 100.
En Nivel de calidad rechazable (RQL o LTPD), ingrese 300.
En Riesgo del productor (alfa), ingrese 0.05.
En Riesgo del consumidor (beta), ingrese 0.10.
En Espec. inferior, ingrese 0,09.
En Desviación estándar histórica, ingrese 0.025.
En Tamaño del lote, ingrese 2500.
Haga clic en Aceptar.

Interpretar los resultados

Para cada lote de 2500 segmentos de tubería, el ingeniero debe seleccionar aleatoriamente y medir el grosor de 104 tubos.

Si Z.LEI es mayor que la distancia crítica, en este caso k = 3,55750, el ingeniero acepta el lote entero. De lo contrario, el ingeniero rechaza todo el lote.

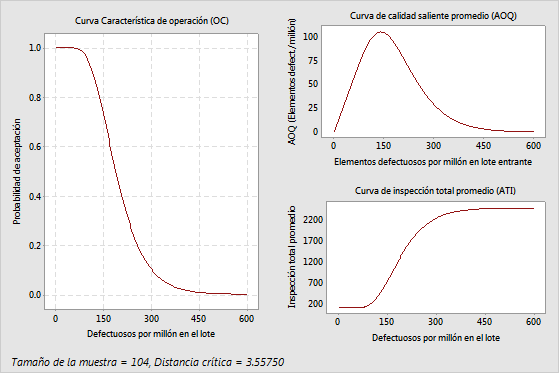
En este caso, la probabilidad de aceptación en el AQL (100 defectuosos por millón) es de 0,95 y la probabilidad de rechazo es de 0,05. El ingeniero y el proveedor convinieron en que los lotes de 100 defectuosos por millón serían aceptados aproximadamente el 95% de las veces, a fin de proteger al productor. La probabilidad de aceptación en el RQL (300 defectuosos por millón) es de 0,10 y la probabilidad de rechazo es de 0,90. El ingeniero y el proveedor convinieron en que los lotes de 300 defectuosos por millón serían rechazados la mayoría de las veces, a fin de proteger al consumidor.

Cuando se rechazan lotes enteros, generalmente se someten a una inspección de 100%, en la que los elementos defectuosos se reemplazan o se reparan. Este tipo de inspección se denomina inspección de rectificación. Utilice las siguientes métricas para comprender el impacto de una inspección de 100% y de reparación:

La calidad saliente promedio (AOQ) representa la calidad promedio del lote después de inspección adicional y reparación. El nivel AOQ es de 91,1 defectuosos por millón en el AQL y 28,6 defectuosos por millón en el RQL. El límite de calidad saliente promedio (AOQL) = 104,6 en 140 defectuosos por millón y representa el nivel de calidad saliente del peor caso.
La inspección total promedio (ATI) representa el número promedio de elementos inspeccionados después de inspección adicional y reparación. La ATI por lote representa el número promedio de segmentos de tubería inspeccionados en un nivel de calidad y probabilidad de aceptación particulares. Para el nivel de calidad de 100, el número total promedio de segmentos de tubería inspeccionados por lote es de 223,2. Para el nivel de calidad de 300, el número total promedio de segmentos de tubería inspeccionados por lote es de 2261,4.

Calidad del lote en elementos defectuosos por millón

Método

Límite de especificación inferior (LEI)	0.09
Desviación histórica estándar	0.025
Tamaño del lote	2500

Nivel de calidad aceptable(AQL)	100
Riesgo del productor(α)	0.05

Nivel de calidad rechazable (RQL o LTPD)	300
Riesgo del consumidor(β)	0.1

Planes generados

Tamaño de la muestra	104
Distancia crítica (valor k)	3.55750

Elementos defectuosos en un millón	Probabilidad de aceptación	Probabilidad de rechazo	AOQ	ATI
100	0.950	0.050	91.1	223.2
300	0.100	0.900	28.6	2261.4

Límite(s) de calidad saliente promedio (AOQL)

AOQL	En defectuosos por millón
104.6	140.0