Una distribución de muestreo describe la probabilidad de obtener cada valor posible de un estadístico de una muestra aleatoria de una población; en otras palabras, qué proporción de todas las muestras aleatorias de ese tamaño ofrecerá ese valor. El procedimiento de bootstrap es un método que estima la distribución de muestreo al tomar múltiples muestras con reemplazo de una sola muestra aleatoria. Estas nuevas muestras se denominan muestras repetidas. Cada muestra tiene el mismo tamaño que la muestra original.
La muestra original representa la población de la cual se extrajo. Por lo tanto, las muestras repetidas de esta muestra original representan lo que obtendríamos si tomáramos muchas muestras de la población. La distribución bootstrap de un estadístico, basada en las muestras repetidas, representa la distribución de muestreo del estadístico.
Por ejemplo, usted desea estimar la distribución de muestreo de la proporción de M&M's azules. Puede abrir un paquete aleatorio y determinar que hay 102 M&M's, de los cuales 23 (22.5%) son azules. El muestreo repetido con reemplazo a partir de esta muestra original imita lo que pudiera ser el aspecto de la población. Para tomar una muestra repetida, se selecciona un M&M aleatoriamente de la muestra original, se registra el color y el M&M es devuelto a la muestra. Esto se realiza 102 veces (el tamaño de la muestra original) para completa una sola muestra repetida. El siguiente gráfico de barras representa una sola muestra bootstrap tomada de la muestra original.
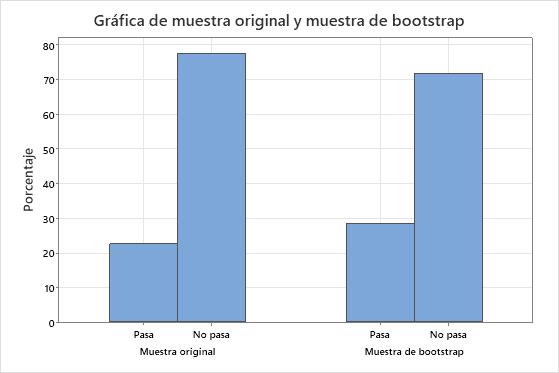
Puesto que la muestra repetida se realiza mediante muestreo con reemplazo, la proporción de la muestra bootstrap generalmente no coincide exactamente con la proporción original. Esta gráfica de barras muestra que la muestra original encontró que aproximadamente 22.5% de los M&M's eran azules, mientras que la muestra bootstrap encontró que aproximadamente 28.4% de los M&M's eran azules. Para crear una distribución bootstrap, usted toma muchos muestras repetidas. El siguiente histograma muestra la distribución bootstrap para 1,000 muestras repetidas del paquete original de M&M's.
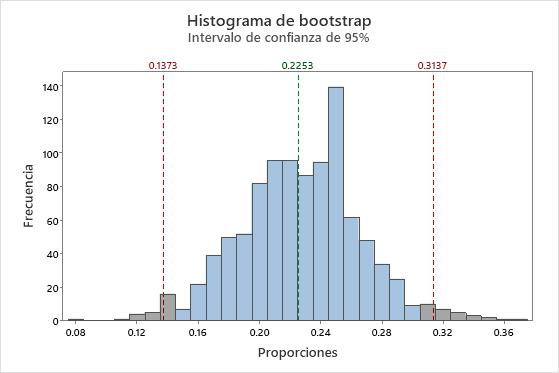
La distribución bootstrap se centra en aproximadamente 22.5%, que es una estimación de la proporción de la población. Las líneas de referencia rojas representan un intervalo de confianza de 95%. El 95% intermedio de los valores de la distribución bootstrap proporciona un intervalo de confianza de 95% para la proporción de la población de M&M's azules. En este ejemplo, usted puede estar 95% seguro de que la proporción de M&M's azules se encuentra entre aproximadamente 13.7% y 31.4%.
Procedimiento bootstrap y el teorema del límite central
El teorema del límite central es un teorema fundamental de probabilidad y estadística. El teorema establece que la distribución de 
, que es la media de una muestra aleatoria de una población con varianza finita, tiene una distribución aproximadamente normal cuando el tamaño de la muestra es grande, independientemente de la forma de la distribución de la población. El procedimiento de bootstrap se puede utilizar para entender fácilmente cómo funciona el teorema del límite central. Considere datos que proceden de una distribución exponencial.
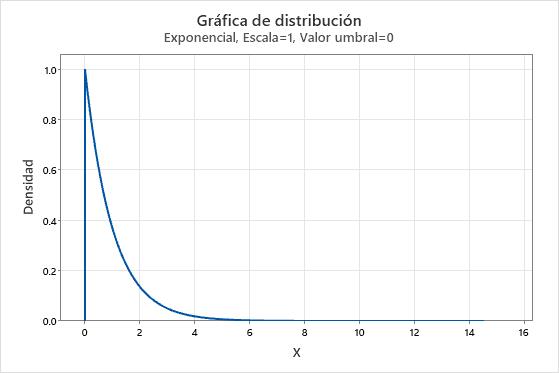
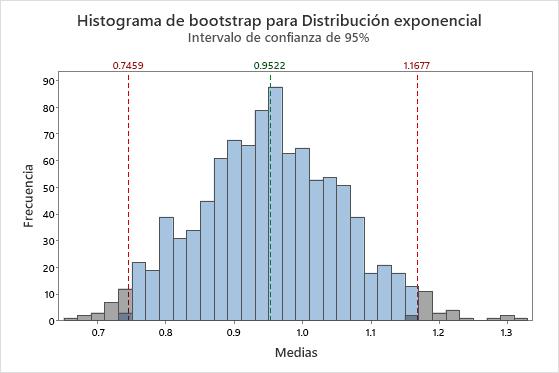
Es muy obvio que los datos son no normales. Pero ahora tomaremos una muestra de 50 observaciones y crearemos una distribución bootstrap de las medias de 10 muestras repetidas.
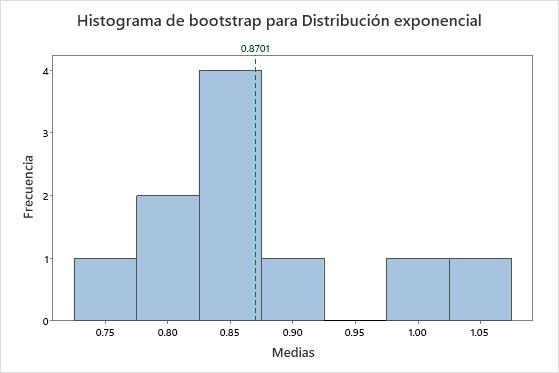
La distribución de las medias es muy diferente de la distribución exponencial. Se parece mucho más a una distribución normal. Este parecido aumenta a medida que aumenta el número de muestras repetidas. Con 1,000 muestras repetidas, la distribución de la media de las muestras repetidas es aproximadamente normal.
