¿Qué es una distribución de Poisson?
La distribución de Poisson se especifica por un parámetro: lambda (λ). Este parámetro es igual a la media y la varianza. Cuando lambda aumente a valores lo suficientemente grandes, la distribución normal (λ, λ) podría utilizarse para aproximar la distribución de Poisson.
Utilice la distribución de Poisson para describir el número de veces que un evento ocurre en un espacio finito de observación. Por ejemplo, una distribución de Poisson puede describir el número de defectos en el sistema mecánico de un avión o el número de llamadas a un centro de llamadas en una hora. La distribución de Poisson se utiliza con frecuencia en el control de calidad, los estudios de fiabilidad/supervivencia y los seguros.
- Los datos son conteos de eventos (enteros no negativos, sin límite superior).
- Todos los eventos son independientes.
- La tasa promedio no cambia durante el período de interés.
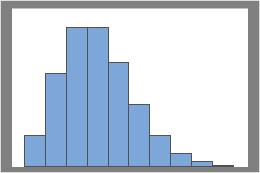
Lambda = 3
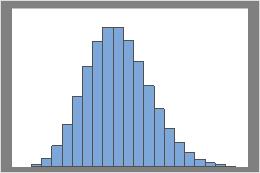
Lambda = 10
¿Qué es tasa de ocurrencia?
La tasa de ocurrencia es igual a la media (λ) dividida entre la dimensión del espacio de observación. Es útil para comparar conteos de Poisson recolectados en diferentes espacios de observación. Por ejemplo, la central telefónica A recibe 50 llamadas telefónicas en 5 horas y la central telefónica B recibe 80 llamadas en 10 horas. Usted no puede comparar directamente estos valores, porque sus espacios de observación son diferentes. Debe calcular la tasa de ocurrencia para comparar estos conteos. La tasa de la central telefónica A es (50 llamadas / 5 horas) = 10 llamadas/hora. La tasa de la central telefónica B es (80 llamadas / 10 horas) = 8 llamadas/hora.
Diferencias entre la distribución de Poisson y la distribución binomial
La distribución de Poisson es similar a la distribución binomial porque ambas modelan conteos de eventos. Sin embargo, dentro de su espacio de observación finito, la distribución de Poisson no establece un límite superior a este conteo: una central telefónica podría recibir un número ilimitado de llamadas en un día y no violar los requisitos de la distribución de Poisson. En cambio, la distribución binomial establece un límite superior en el conteo: el número de eventos que usted observa no puede exceder el número de ensayos que realiza.
