Distribución exponencial

Utilice la distribución exponencial para modelar el tiempo entre eventos en un proceso continuo de Poisson. Se presupone que eventos independientes ocurren a una tasa constante.

Esta distribución tiene una amplia gama de aplicaciones, que incluyen el análisis de fiabilidad de productos y sistemas, teorías de colas y cadenas de Markov.

Por ejemplo, la distribución exponencial se puede utilizar para modelar:

Cuánto tiempo tarda en fallar un componente electrónico
El intervalo de tiempo entre las llegadas de clientes a una terminal
El tiempo que esperan los clientes en fila hasta recibir servicio
El tiempo hasta que se declara el incumplimiento de un pago (modelos de riesgo de crédito).
El tiempo para desintegración de un núcleo radiactivo

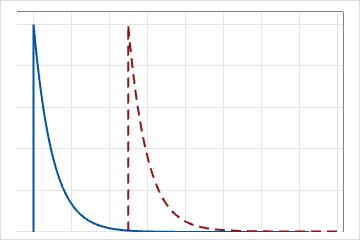
La distribución exponencial de 2 parámetros se define por sus parámetros de escala y valor umbral. El parámetro de valor umbral, θ, si es positivo, desplaza la distribución una distancia θ a la derecha. Por ejemplo, usted está interesado en estudiar la falla de un sistema con θ = 5. Esto significa que las fallas comienzan a ocurrir solo después de 5 horas de funcionamiento y no pueden ocurrir antes. En la siguiente gráfica, el parámetro de valor umbral, θ, es igual a 5 y desplaza la distribución 5 unidades a la derecha.

Para la distribución exponencial de 1 parámetro, el valor umbral es cero y la distribución se define por su parámetro de escala. Para la distribución exponencial de 1 parámetro, el parámetro de escala es igual a la media.

¿Qué significa "sin memoria"?

Una propiedad importante de la distribución exponencial es que no tiene memoria. La probabilidad de un evento no depende de los ensayos anteriores. Por lo tanto, la tasa de ocurrencia se mantiene constante.

La propiedad de ausencia de memoria indica que la vida útil restante de un componente no depende de su antigüedad actual. Por ejemplo, ensayos aleatorios de lanzamientos al aire de una moneda demuestran la propiedad de ausencia de memoria. Un sistema que experimenta un desgaste natural y, por lo tanto, tiene más probabilidades de fallar más tarde en su vida útil no es un sistema sin memoria.