Ejemplo de uso de la ICDF para determinar períodos de garantía
Por ejemplo, un fabricante de electrodomésticos investiga los tiempos de falla de las resistencias de sus tostadores. Este fabricante desea determinar el tiempo que debe transcurrir para que fallen proporciones específicas de las resistencias, a fin de poder establecer el período de garantía. Los tiempos de falla del elemento de generación de calor siguen una distribución normal, con una media de 1000 horas y una desviación estándar de 300 horas. La función de densidad de probabilidad ayuda a identificar regiones de mayores y menores probabilidades de falla. La CDF inversa proporciona el tiempo de falla correspondiente para cada probabilidad acumulada.
Utilice la CDF inversa para estimar el tiempo que transcurre para que falle el 5% de los componentes de generación de calor, los tiempos entre los cuales fallará el 95% de todos los componentes de generación de calor o el tiempo que transcurre para que solo persista el 5% de los componentes de generación de calor. La CDF inversa para probabilidades acumuladas específicas es igual al tiempo de falla en el lado derecho del área sombreada por debajo de la curva PDF.
Determinar el tiempo que transcurre para que falle el 5%
- Elija .
- Elija Probabilidad acumulada inversa. En Media, ingrese 1000. En Desviación estándar, ingrese 300. En Constante de entrada, ingrese 0.05.
- Haga clic en Aceptar.
El tiempo para el cual se espera que haya fallado el 5% de las resistencias es la CDF inversa de 0,05 o 506,544 horas.
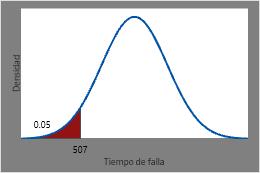
Esta gráfica ilustra la CDF inversa.
Determinar los tiempos entre los cuales fallará el 95%
- Elija .
- Elija Probabilidad acumulada inversa. En Media, ingrese 1000. En Desviación estándar, ingrese 300. En Constante de entrada, ingrese 0.025. Haga clic en Aceptar.
El tiempo para el cual se espera que haya fallado el 2.5% de las resistencias es la CDF inversa de 0,025 o 412 horas.
- Repita el paso 2, pero ingrese 0,975 en lugar de 0,025. Haga clic en Aceptar.El tiempo para el cual se espera que haya fallado el 97.5% de las resistencias es la CDF inversa de 0,975 o 1588 horas.
Por lo tanto, los tiempos entre los cuales se espera que falle el 95% de todas las resistencias es la CDF inversa de 0,025 y la CDF inversa de 0,975 o 412 horas y 1588 horas.
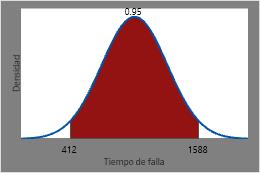
Esta gráfica ilustra la CDF inversa.
Determinar el tiempo en el que el 5% seguirá funcionando
- Elija .
- Elija Probabilidad acumulada inversa. En Media, ingrese 1000. En Desviación estándar, ingrese 300. En Constante de entrada, ingrese 0.95.
- Haga clic en Aceptar.
El tiempo que se espera que transcurra para que solo el 5% de las resistencias siga funcionando es la CDF inversa de 0,95 o 1493 horas.
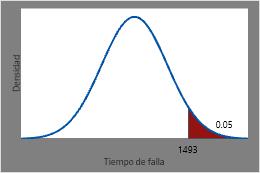
Esta gráfica ilustra la CDF inversa.
Ejemplo de uso de la CDF y la ICDF con la distribución hipergeométrica
Cuando usted intenta determinar la probabilidad acumulada inversa de una distribución discreta, la salida contiene dos conjuntos de columnas.
Supongamos que tienes la inversa de la probabilidad acumulada de una proporción, p. El primer conjunto de columnas en la salida muestra el mayor x tal que P(X ≤ x) ≤ p. El segundo conjunto de columnas lista el x más pequeño tal que P(X ≤ x) ≥ p.
Calcular la probabilidad acumulada de una distribución hipergeométrica
- En la columna C1 de la hoja de trabajo, ingrese 0 1 2.
C1 0 1 2 - Elija .
- Elija Probabilidad acumulada.
- En Tamaño de la población (N), escribe 20000.
- En Conteo de eventos en la población (M), escribe 2000.
- En Tamaño de la muestra (n), escribe 20.
- Elige Columna de entrada e introduce C1. Haga clic en Aceptar.
Función de distribución acumulada
- P(X ≤ 0) = 0,121448. La probabilidad de obtener 0 defectos es de aproximadamente 12%.
- P(X ≤ 1) = 0,391619. La probabilidad de obtener 0 o 1 defecto es aproximadamente 39%.
- P(X ≤ 2) = 0,676941. La probabilidad de obtener 0, 1 o 2 defectos es aproximadamente 68%.
Calcular la probabilidad acumulada inversa de una distribución hipergeométrica
Ahora que conoce las probabilidades acumuladas asociadas con el número de defectos, calcule la probabilidad acumulada inversa.
Supongamos que usted desea calcular el número de defectos, x, tal que la probabilidad acumulada, p, sea 0,50. A partir de los resultados previos, usted sabe que P(X ≤ 1 ) = 0,391619 y que P(X ≤ 2 ) = 0,676941. Dado que la distribución hipergeométrica es discreta, el número de defectos no puede estar entre 1 y 2. En otras palabras, puede que tengas 1 defecto o 2, pero no 1,4 defectos. Por lo tanto, si eliges Constante de entrada e introduces 0,50, Minitab calcula ambas probabilidades en la salida, como se muestra en el siguiente ejemplo:
- Elija .
- Elija Probabilidad acumulada inversa.
- En Tamaño de la población (N), escribe 20000.
- En Conteo de eventos en la población (M), escribe 2000.
- En Tamaño de la muestra (n), escribe 20.
- Elige Constante de entrada, y escribe 0,50. Haga clic en Aceptar.
Función de distribución acumulada inversa
La primera probabilidad indica un valor de x tal que P(X ≤ x) < p and the second probability indicates the smallest x such that P(X ≤ x) ≥ p. In this example, the first probability shows the largest number of defectives, x = 2, such that P(X ≤ 2) <0.5 and the 2nd muestra el menor número de defectuosos, x = 3, tal que P(X ≤ 3) ≥ 0,5.
Utilizar la ICDF para calcular valores críticos
Puede utilizar Minitab para calcular un valor crítico para una prueba de hipótesis en lugar de buscar en una tabla.
Supongamos que usted realiza una prueba de chi-cuadrada con un α = 0,02 y 12 grados de libertad. ¿Cuál es el valor crítico correspondiente? Un nivel de significancia (α) = 0,02 corresponde a un valor de probabilidad acumulada de 1 – 0,02 = 0,98.
- Elija .
- Elija Probabilidad acumulada inversa.
- En Grados de libertad, ingrese 12.
- Elige Constante de entrada e introduce 0,98.
- Haga clic en Aceptar.
Minitab muestra el valor crítico, 24.054. Para la prueba de chi-cuadrada, si el estadístico de prueba es mayor que el valor crítico, usted puede concluir que hay evidencia estadística para rechazar la hipótesis nula.
Nota
Este ejemplo utiliza la distribución de chi-cuadrada. Sin embargo, siga estos mismos pasos para cualquier distribución que seleccione.
