¿Qué es la función de distribución acumulada (CDF)?
La función de distribución acumulada (CDF) calcula la probabilidad acumulada de un valor dado de x. Utilice la CDF para determinar la probabilidad de que una observación aleatoria que se toma de la población sea menor que o igual a cierto valor. También puede usar esta información para determinar la probabilidad de que una observación sea mayor que cierto valor o se encuentre entre dos valores.
Ejemplo de uso de la CDF para evaluar pesos de llenado
Por ejemplo, los pesos de llenado de una lata de gaseosa siguen una distribución normal, con una media de 12 onzas y una desviación estándar de 0.25 onzas. La función de densidad de probabilidad (PDF) describe la probabilidad de valores posibles de peso de llenado. La CDF proporciona la probabilidad acumulada de cada valor de x.
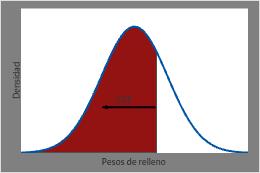
La CDF para pesos de llenado en cualquier punto específico es igual al área que se encuentra por debajo de la curva PDF a la izquierda de ese punto.
Utilice la CDF para determinar la probabilidad de que una lata de gaseosa seleccionada aleatoriamente tenga un peso de llenado menor que 11.5 onzas, mayor que 12.5 onzas o entre 11.5 y 12.5 onzas.
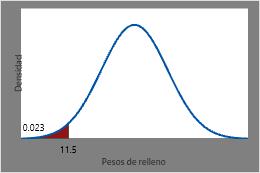
La probabilidad de que una lata de gaseosa seleccionada aleatoriamente tenga un peso de llenado menor que o igual a 11.5 onzas es la CDF en 11.5 o aproximadamente 0.023.
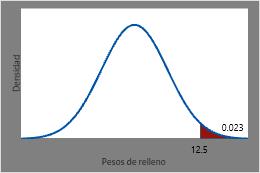
La probabilidad de que una lata de gaseosa seleccionada aleatoriamente tenga un peso de llenado mayor que 12.5 onzas es 1 menos la CDF en 12.5 (0.977) o aproximadamente 0.023.
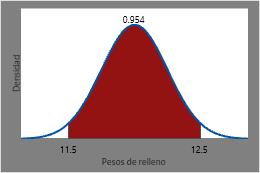
La probabilidad de que una lata de gaseosa seleccionada aleatoriamente tenga un peso de llenado entre 11.5 onzas y 12.5 onzas es la CDF en 12.5 menos la CDF en 11.5 o aproximadamente 0.954.
Utilizar la CDF para calcular valores p
Para calcular un valor p para una prueba F, primero debe calcular la función de distribución acumulada (CDF). El valor p es 1 – CDF.
Supongamos que usted realiza un análisis de regresión lineal múltiple con los siguientes grados de libertad: GL (Regresión) = 3; GL (Error) = 25; y el estadístico F = 2.44.
Calcular un valor p para la prueba F
- Elija .
- Elija Probabilidad acumulada.
- En Parámetro de no centralidad, ingrese 0.
- En Grados de libertad del numerador, ingrese 3.
- En Grados de libertad del denominador, ingrese 25.
- Elija Constante de entrada e ingrese 2.44.
- En Almacenamiento opcional, ingrese K1. Haga clic en Aceptar. K1 contiene la función de distribución acumulada.
Utilizar la Calculadora para restar el valor p a 1
- Elija .
- En Almacenar resultado en variable, ingrese el Valor p.
- En Expresión, ingrese 1-K1. Haga clic en Aceptar.
Nota
Este ejemplo es para una distribución F; sin embargo, puede utilizar un método similar para otras distribuciones.
