En este tema
Histograma
Un histograma divide valores de la muestra entre muchos intervalos y representa la frecuencia de los valores de los datos en cada intervalo con una barra.
Interpretación
50 muestras repetidas
1000 muestras repetidas
La distribución suele ser más fácil de determinar con más muestras repetidas. Por ejemplo, en estos datos, la distribución es ambigua para 50 muestras repetidas. Con 1000 muestras repetidas, la forma parece aproximadamente normal.
El histograma muestra visualmente los resultados de la prueba de hipótesis. Minitab ajusta los datos para que el centro de las muestras repetidas sea el mismo de la media hipotética. Para una prueba unilateral, se traza una línea de referencia en la media de la muestra original. Para una prueba bilateral, se traza una línea de referencia en la media de la muestra original y a la misma distancia del lado opuesto de la media hipotética. El valor p es la proporción de medias de muestras que son más extremas que los valores en las líneas de referencia. En otras palabras, el valor p es la proporción de medias de muestras que son tan extremas como su muestra original cuando usted presupone que la hipótesis nula es verdadera. Estas medias aparecen en color rojo en el histograma.
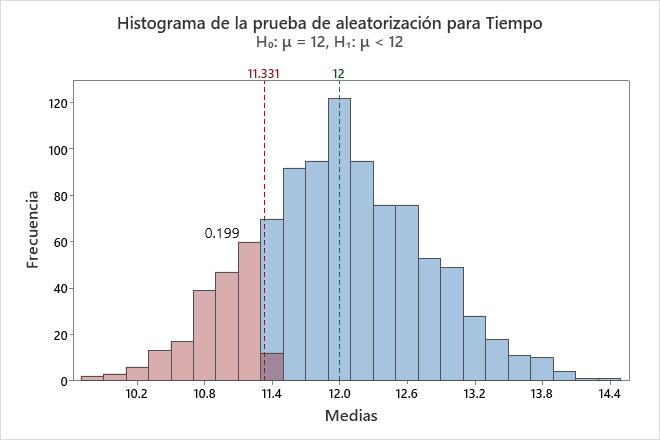
En este histograma, la distribución bootstrap parece ser normal. El valor p de 0.2030 indica que 20.3% de las medias de las muestras es menor que la media de la muestra original.
Gráfica de valores individuales
Una gráfica de valores individuales muestra los valores individuales en la muestra. Cada círculo representa una observación. Una gráfica de valores individuales es especialmente útil cuando usted tiene relativamente pocas observaciones y también cuando debe evaluar el efecto de cada observación.
Nota
Minitab muestra una gráfica de valores individuales solamente cuando usted toma solo una muestra repetida. Minitab muestra tanto los datos originales como los datos de la muestra repetida.
Interpretación
Minitab ajusta los datos para que el centro de las muestras repetidas sea el mismo de la media hipotética. Primero, Minitab calcula la diferencia entre la media hipotética y la media de la muestra original. Luego Minitab suma o resta la diferencia de cada valor en la muestra original. Las muestras repetidas se toman de estos datos ajustados.
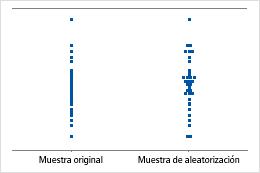
La media de la muestra es igual a la media hipotética
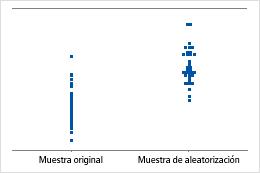
La media de la muestra es 2 desviaciones estándar menos que la media hipotética
Hipótesis nula e hipótesis alternativa
- Hipótesis nula
- La hipótesis nula indica que un parámetro de población (tal como la media, la desviación estándar, etc.) es igual a un valor hipotético. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.
- Hipótesis alternativa
- La hipótesis alternativa indica que un parámetro de población es más pequeño, más grande o diferente del valor hipotético de la hipótesis nula. La hipótesis alternativa es lo que usted podría pensar que es cierto o espera probar que es cierto.
Interpretación
En la salida, las hipótesis nula y alternativa le ayudan a verificar que usted ingresó el valor correcto de la media hipotética.
Muestra observada
| Variable | N | Media | Desv.Est. | Varianza | Suma | Mínimo | Mediana | Máximo |
|---|---|---|---|---|---|---|---|---|
| Tiempo | 16 | 11.331 | 3.115 | 9.702 | 181.300 | 7.700 | 10.050 | 16.000 |
Prueba de aleatorización
| Hipótesis nula | H₀: μ = 12 |
|---|---|
| Hipótesis alterna | H₁: μ < 12 |
| Número de remuestreos | Media | Desv.Est. | Valor p |
|---|---|---|---|
| 1000 | 11.9783 | 0.7625 | 0.199 |
En estos resultados, la hipótesis nula es que la media de la población es igual a 12. La hipótesis alternativa es que la media es menor que 12.
Número de remuestreos
El número de remuestreos es el número de veces que Minitab toma una muestra aleatoria con reemplazo del conjunto de datos original. Generalmente, un número elevado de remuestreos funciona mejor.
Minitab ajusta los datos para que el centro de los remuestreos sea el mismo de la media hipotética. Primero, Minitab calcula la diferencia entre la media hipotética y la media de la muestra original. Luego Minitab suma o resta la diferencia de cada valor en la muestra original. Los remuestreos se toman de estos datos ajustados. El tamaño de la muestra de cada remuestreo es igual al tamaño de la muestra del conjunto de datos original. El número de remuestreos es igual al número de observaciones en el histograma.
Media
La media es la suma de todas las medias en la muestra bootstrap dividida entre el número de remuestreos. Minitab ajusta los datos para que el centro de los remuestreos sea el mismo de la media hipotética.
Interpretación
Minitab muestra dos valores de media diferentes, la media de la muestra observada y la media de la distribución bootstrap. La media de la muestra observada es una estimación de la media de población. La media de la distribución boostrap generalmente es cercana a la media hipotética. Cuanto mayor sea la diferencia entre estos dos valores, más evidencia esperaría usted contra la hipótesis nula.
Desv.Est. (muestra bootstrap)
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido. Debido a que la desviación estándar utiliza las mismas unidades que los datos, generalmente es más fácil de interpretar que la varianza.
La desviación estándar de las muestras bootstrap (también conocida como el error estándar bootstrap) es una estimación de la desviación estándar de la distribución de muestreo de la media. Puesto que el error estándar bootstrap es la variación de medias de muestra, mientras que la desviación estándar de las muestras observadas es la variación de observaciones individuales, el error estándar bootstrap es más pequeño.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersas están las medias de la muestra bootstrap con respecto a la media general. Un valor de desviación estándar más alto indica una mayor dispersión de las medias. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media general, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
Utilice la desviación estándar de las muestras bootstrap para estimar la precisión de las medias bootstrap. Un valor menor indica más precisión. Una desviación estándar mayor en la muestra original generalmente da como resultado un error estándar bootstrap mayor y una prueba de hipótesis menos potente. Un tamaño de muestra menor generalmente también da como resultado un error estándar bootstrap mayor y una prueba de hipótesis menos potente.
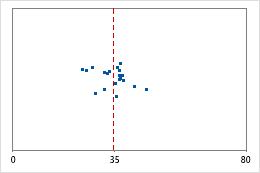
Hospital 1
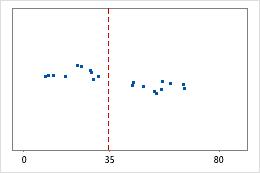
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Valor p
El valor p es la proporción de medias de muestras que son tan extremas como su muestra original cuando usted presupone que la hipótesis nula es verdadera. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si la media de la población es estadísticamente diferente de la media hipotética.
- Valor p ≤ α: La diferencia entre las medias es estadísticamente significativa (Rechazar H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula. Usted puede concluir que la diferencia entre la media de la población y la media hipotética es estadísticamente significativa. Para calcular un intervalo de confianza y determinar si la diferencia es significativa desde el punto de vista práctico, utilice Remuestreo bootstrap para función de 1 muestra. Para obtener más información, vaya a Significancia estadística y significancia práctica.
- Valor p > α: La diferencia entre las medias no es estadísticamente significativa (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que la diferencia entre media de la población y la media hipotética es estadísticamente significativa.
