Soporte de Minitab® 

Seleccione la distribución e ingrese los parámetros

Más información sobre Minitab
Elija Calc > Datos aleatorios, luego seleccione la distribución e ingrese los parámetros.

En este tema

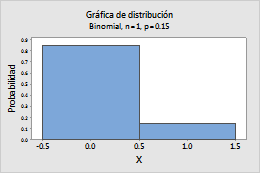
Bernoulli

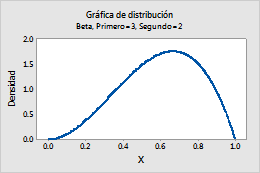
En Probabilidad del evento, ingrese un número entre 0 y 1 para la probabilidad de que ocurra el resultado de interés. Una ocurrencia se denomina un "evento". Para obtener más información, vaya a Distribución de Bernoulli.
Utilice la distribución de Bernoulli cuando un proceso aleatorio tenga exactamente dos resultados: evento o no evento. Las secuencias de ensayos de Bernoulli independientes generan las demás distribuciones, como la distribución binomial, que modela el número de éxitos en n ensayos. Por ejemplo, esta gráfica representa una muestra aleatoria de una distribución binomial que tiene 1 evento y una probabilidad de evento de 0.15.

Beta

Complete los siguientes pasos para ingresar los parámetros para la Distribución beta.

  1. En Primer parámetro de forma, ingrese un número que sea mayor que cero para el primer parámetro de forma.
  2. En Segundo parámetro de forma, ingrese un número que sea mayor que cero para el segundo parámetro de forma.

Por ejemplo, esta gráfica muestra una distribución beta que tiene una primera forma de 3 y una segunda forma de 2.

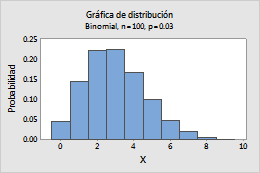
Binomial

Complete los siguientes pasos para ingresar los parámetros para la Distribución binomial.

  1. En Número de ensayos, ingrese el tamaño de la muestra.
  2. En Probabilidad del evento, ingrese un número entre 0 y 1 para la probabilidad de que ocurra el resultado de interés. Una ocurrencia se denomina un "evento".

Por ejemplo, esta gráfica muestra una distribución binomial que tiene 100 ensayos y una probabilidad de evento de 0.03.

Cauchy

Complete los siguientes pasos para ingresar los parámetros para la Distribución de Cauchy.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución.

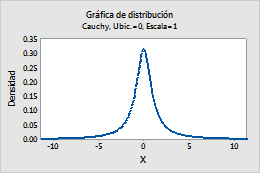
Por ejemplo, esta gráfica muestra una distribución de Cauchy que tiene una ubicación de 0 y una escala de 1.

Chi-cuadrada

En Grados de libertad, ingrese el número de grados de libertad que definen la Distribución de chi-cuadrada.

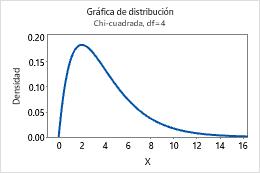
Por ejemplo, esta gráfica muestra una distribución de chi-cuadrada que tiene 4 grados de libertad.

Discreta

Complete los siguientes pasos para ingresar los parámetros para la Distribución discreta.

  1. En Valores en, ingrese la columna que contiene los valores que se incluirán en la distribución. Generalmente, los valores son eventos o conteos discretos que se representan con valores numéricos.
  2. En Probabilidades en, ingrese la columna que contiene las probabilidades de cada valor. Las probabilidades deben estar entre 0 y 1 y deben sumar 1.

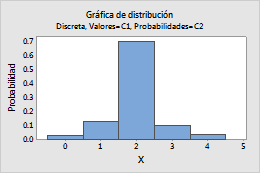
En esta hoja de trabajo, Valor contiene los conteos que se incluirán en la distribución y Probabilidad contiene la probabilidad de cada conteo.

C1 C2
Valor Probabilidad
0 0.03
1 0.13
2 0.70
3 0.10
4 0.04

Exponencial

Complete los siguientes pasos para ingresar los parámetros para la Distribución exponencial.

  1. En Escala, ingrese el parámetro de escala. El parámetro de escala es igual a la media cuando el parámetro de valor umbral es igual a 0.
  2. En Valor umbral, ingrese el borde inferior de la distribución.

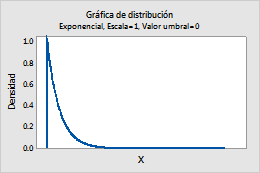
Por ejemplo, esta gráfica muestra una distribución exponencial que tiene una escala de 1 y un valor umbral de 0.

F

En Grados de libertad del numerador y Grados de libertad del denominador, ingrese los grados de libertad del numerador y del denominador para definir la distribución F. Para obtener más información, vaya a Distribución F.

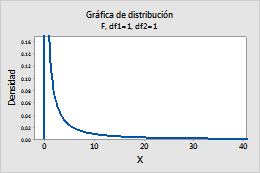
Por ejemplo, esta gráfica muestra un distribución F que tiene 1 grado de libertad del numerador y 1 grado de libertad del denominador.

Gamma

Complete los siguientes pasos para ingresar los parámetros para la Distribución gamma.

  1. En Parámetro de forma, ingrese el valor que represente la forma de la distribución.
  2. En Parámetro de escala, ingrese el valor que represente la escala de la distribución.
  3. En Parámetro de umbral, ingrese el borde inferior de la distribución.

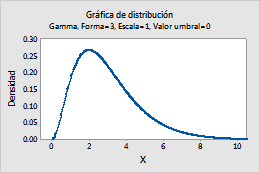
Por ejemplo, esta gráfica muestra una distribución gamma que tiene una forma de 3, una escala de 1 y un valor umbral de 0.

Geométrica

Complete los siguientes pasos para ingresar los parámetros para la Distribución geométrica.

  1. En Probabilidad del evento, ingrese un número entre 0 y 1 para la probabilidad de ocurrencia en cada ensayo. Una ocurrencia se conoce como un "evento".
  2. Para especificar qué versión de la distribución geométrica utilizar, haga clic en Opciones y seleccione una de las siguientes opciones:
    • Modelar el número total de ensayos: Modelar el número total de ensayos necesarios para producir un evento.
    • Modelar solamente el número de eventos fallidos: Modelar el número de no eventos que ocurren antes de que ocurra un evento.
    Sugerencia

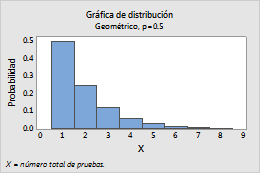
    Para cambiar la configuración predeterminada para sesiones futuras de Minitab, elija Archivo > Opciones > Comandos individuales > Distribuciones.

Por ejemplo, esta gráfica muestra una distribución geométrica que modela el número total de ensayos y tiene una probabilidad de evento de 0,5.

Hipergeométrica

Complete los siguientes pasos para ingresar los parámetros para la Distribución hipergeométrica.

  1. En Tamaño de la población (N), ingrese el número total de elementos de la población (N). Cuando N es demasiado grande para que sea conocido, la distribución binomial se aproxima a la distribución hipergeométrica.
  2. En Conteo de eventos en la población (M), ingrese un número entre 0 y N (tamaño de la población) que represente el número de eventos en la población.
  3. En Tamaño de la muestra (n), ingrese el número de elementos que se toman para la muestra sin reemplazo.

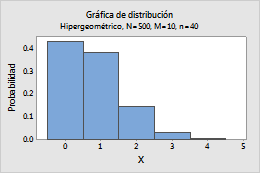
Por ejemplo, esta gráfica muestra una distribución hipergeométrica que tiene una población de 400, un conteo de eventos de 10 y un tamaño de muestra de 40.

Enteros

Complete los siguientes pasos para ingresar los parámetros para la Distribución de enteros.

  1. En Valor mínimo, ingrese la cota inferior de la distribución.
  2. En Valor máximo, ingrese la cota superior de la distribución.

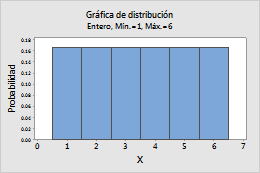
Por ejemplo, esta gráfica muestra un distribución de enteros que tiene un valor mínimo de 1 y un valor máximo de 6.

Laplace

Complete los siguientes pasos para ingresar los parámetros para la Distribución de Laplace.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución.

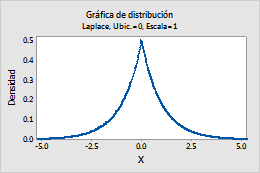
Por ejemplo, esta gráfica muestra una distribución de Laplace que tiene una ubicación de 0 y una escala de 1.

Valor extremo más grande

Complete los siguientes pasos para ingresar los parámetros para la distribución de valor extremo más grande. Para obtener más información, vaya a Distribuciones de valor extremo más pequeño y más grande.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución.

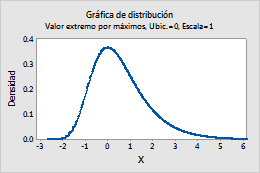
Por ejemplo, esta gráfica muestra una distribución de valor extremo más grande que tiene una ubicación de 0 y una escala de 1.

Logística

Complete los siguientes pasos para ingresar los parámetros para la Distribución logística.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución.

Por ejemplo, esta gráfica muestra una distribución logística que tiene una ubicación de 0 y una escala de 1.

Loglogística

Complete los siguientes pasos para ingresar los parámetros para la Distribución loglogística.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución logística relacionada.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución logística relacionada.
  3. En Valor umbral, ingrese el borde inferior de la distribución.

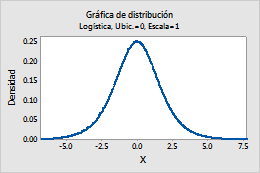
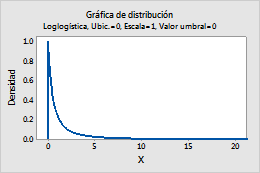
Por ejemplo, esta gráfica muestra una distribución loglogística que tiene una ubicación de 0, una escala de 1 y un valor umbral de 0.

Lognormal

Complete los siguientes pasos para ingresar los parámetros para la Distribución lognormal.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución normal relacionada.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución normal relacionada.
  3. En Valor umbral, ingrese el borde inferior de la distribución.

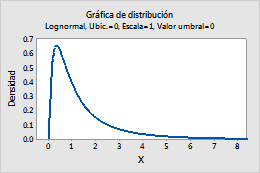
Por ejemplo, esta gráfica muestra una distribución lognormal que tiene una ubicación de 0, una escala de 1 y un valor umbral de 0.

Normal multivariada

Complete los siguientes pasos para ingresar los parámetros para la Distribución normal multivariada.

  1. En Columna con la media, ingrese la columna que contiene el vector de medias.
  2. En Matriz de varianza-covarianza, ingrese la matriz (por ejemplo, M1) que contiene las varianzas y las covarianzas de las variables en el mismo orden que en la columna que contiene las medias.

En este ejemplo, los datos provienen de tres variable aleatorias normales correlacionadas. Las medias están en C1 y la matriz de varianzas y covarianzas está en las columnas C2–C4.

C1 C2 C3 C4
       
2.0 13.0321 2.6544 0.0899
100.1 2.6544 6.5883 1.4438
151.3 0.0899 1.4438 12.2219

Primero, Minitab debe leer la matriz de varianzas y covarianzas y almacenarla.
  1. Elija Datos > Copiar > Columnas a matriz.
  2. En Copiar desde columnas, ingrese C2-C4.
  3. En Almacenar datos copiados, en En hoja de trabajo actual, en matriz:, ingrese M1.
  4. Haga clic en Aceptar.

Ahora, usted puede generar datos aleatorios a partir de la distribución normal multivariada.

  1. Elija Calc > Datos aleatorios > Normal multivariada.
  2. En Número de filas de datos que se generarán, ingrese el número de filas que desee. En este ejemplo, ingrese 18.
  3. En Almacenar en columna, ingrese las columnas de almacenamiento. En este ejemplo, ingrese C6-C8.
  4. En Columna con la media, ingrese la columna que contiene las medias. En este ejemplo, ingrese C1.
  5. En Matriz de varianza-covarianza, ingrese la matriz. En este ejemplo, ingrese M1.
  6. Haga clic en Aceptar.
Sugerencia

Para obtener la misma muestra que en la tabla de abajo, establezca la base del generador aleatorio antes de generar la muestra aleatoria. Elija Calc > Establecer base e ingrese 5.

C6 C7 C8
     
1.61033 99.192 148.814
0.45883 96.093 144.679
−0.46745 101.041 148.936
… … …

Binomial negativa

Complete los siguientes pasos para ingresar los parámetros para la Distribución binomial negativa.

  1. En Probabilidad del evento, ingrese un número entre 0 y 1 para la probabilidad de ocurrencia en cada ensayo. Una ocurrencia se conoce como un "evento".
  2. En Número de eventos necesarios, ingrese un entero positivo que represente el número de veces que debe ocurrir el evento.
  3. Para especificar qué versión de la distribución binomial negativa utilizar, haga clic en Opciones y seleccione una de las siguientes opciones:
    • Modelar el número total de ensayos: Modelar el número total de ensayos necesarios para producir el número especificado de eventos.
    • Modelar solamente el número de eventos fallidos: Modelar el número de no eventos que deben ocurrir para que ocurra el número especificado de eventos.
    Sugerencia

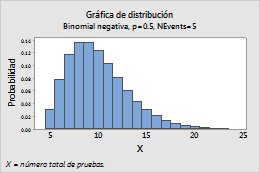
    Para cambiar la configuración predeterminada para sesiones futuras de Minitab, elija Archivo > Opciones > Comandos individuales > Distribuciones.

Por ejemplo, esta gráfica muestra una distribución binomial negativa que modela el número total de ensayos y tiene una probabilidad de evento de 0,5 y 5 eventos.

Normal

Complete los siguientes pasos para ingresar los parámetros para la Distribución normal.

  1. En Media, ingrese el valor del centro de la distribución.
  2. En Desviación estándar, ingrese el valor de la dispersión de la distribución.

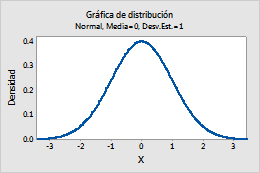
Por ejemplo, esta gráfica muestra una distribución normal que tiene una media de 0 y una desviación estándar de 1.

Poisson

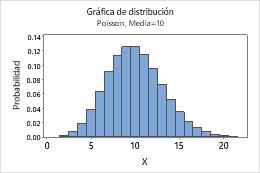
En Media, ingrese el valor de la tasa promedio de ocurrencia. Para obtener más información, vaya a Distribución de Poisson.

Por ejemplo, esta gráfica muestra una distribución de Poisson que tiene una media de 10.

Valor extremo más pequeño

Complete los siguientes pasos para ingresar los parámetros para la distribución del valor extremo más pequeño. Para obtener más información, vaya a Distribuciones de valor extremo más pequeño y más grande.

  1. En Ubicación, ingrese un valor que represente la ubicación del pico de la distribución.
  2. En Escala, ingrese un valor que represente la dispersión de la distribución.

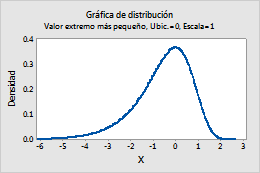
Por ejemplo, esta gráfica muestra una distribución del valor extremo más pequeño que tiene una ubicación de 0 y una escala de 1.

t

En Grados de libertad, ingrese los grados de libertad para definir la distribución t. Para obtener más información, vaya a Distribución t.

Por ejemplo, esta gráfica muestra una distribución t que tiene 2 grados de libertad.

Triangular

Complete los siguientes pasos para ingresar los parámetros para la Distribución triangular.

  1. En Cota inferior, ingrese el valor mínimo de la distribución.
  2. En Moda, ingrese el valor del pico de la distribución.
  3. En Cota superior, ingrese el valor máximo de la distribución.

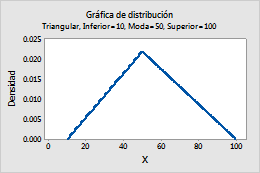
Por ejemplo, esta gráfica muestra una distribución triangular que tiene una cota inferior de 10, una moda de 50 y una cota superior de 100.

Uniforme

Complete los siguientes pasos para ingresar los parámetros para la Distribución uniforme.

  1. En Cota inferior, ingrese el valor mínimo de la distribución.
  2. En Cota superior, ingrese el valor máximo de la distribución.

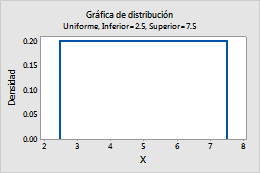
Por ejemplo, esta gráfica muestra una distribución uniforme que tiene una cota inferior de 2.5 y una cota superior de 7.5.

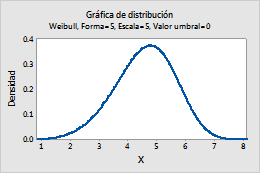
Weibull

Complete los siguientes pasos para ingresar los parámetros para la Distribución de Weibull.

  1. En Parámetro de forma, ingrese el valor que represente la forma de la distribución.
  2. En Parámetro de escala, ingrese el valor que represente la escala de la distribución.
  3. En Parámetro de umbral, ingrese el borde inferior de la distribución.

Por ejemplo, esta gráfica muestra una distribución de Weibull que tiene una ubicación de 5, una escala de 5 y un valor umbral de 0.

Copyright © 2024 Minitab, LLC. All rights Reserved.