Métodos y fórmulas para Remuestreo bootstrap para función de 1 muestra

Una medida frecuentemente utilizada del centro de un lote de números. La media también se denomina promedio. Es la suma de todas las observaciones dividida entre el número de observaciones (presentes).

Fórmula

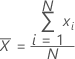
Notación

Término	Description
xi	i ésima observación
N	número de observaciones presentes

La desviación estándar de la muestra proporciona una medida de la dispersión de los datos. Es igual a la raíz cuadrada de la varianza de la muestra.

Fórmula

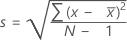
Notación

Término	Description
x i	i ésima observación
	media de las observaciones
N	número de observaciones presentes

La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.

Fórmula

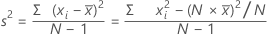
Notación

Término	Description
xi	iésima observación
	media de las observaciones
N	número de observaciones presentes

Fórmula

Notación

Término	Description
xi	i ésima observación

El valor más pequeño del conjunto de datos.

La mediana de la muestra está en la mitad de los datos: por lo menos la mitad de las observaciones es menor que o igual a la mediana y por lo menos la mitad de las observaciones es mayor que o igual a la mediana.

Supongamos que usted tiene una columna que contiene N valores. Para calcular la mediana, primero ordene los valores de los datos del más pequeño al más grande. Si N es impar, la mediana de la muestra es el valor del medio. Si N es par, la mediana es el promedio de los dos valores del medio.

Por ejemplo, cuando N = 5 y usted tiene los datos x₁, x₂, x₃, x₄ y x₅, la mediana = x₃.

Cuando N = 6 y usted ordenó los datos x₁, x₂, x₃, x₄, x₅ y x₆:

donde x₃ y x₄ son la tercera y la cuarta observación

El valor más grande del conjunto de datos.

Cuando el estadístico seleccionado es una proporción, Minitab muestra la proporción de la muestra observada.

Fórmula

Notación

Término	Description
x	número de eventos en la muestra original
N	número de ensayos en la muestra original

Fórmula

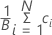
Notación

Término	Description
ci	estadístico elegido de la iésima muestra repetida
B	número de muestras repetidas
N	número de observaciones en la muestra original

Si el estadístico elegido es una proporción, Minitab no calcula la desviación estándar.

Fórmula

Notación

Término	Description
	media del estadístico elegido de los remuestreos
B	número de remuestreos
ci	estadístico elegido del iesimo remuestreo

Fórmula

Ordene el estadístico elegido de los remuestreos en orden creciente. x₁ es el número más bajo, x_B es el número más alto.

Borde inferior: x_l donde =

Borde superior: x_u donde =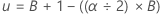

Para analizar una proporción, Minitab no toma remuestreos de la columna original de datos. En su lugar, Minitab realiza los remuestreos tomando muestras aleatorias de una distribución binomial. El número de ensayos y la probabilidad del evento para la distribución se toman de la muestra original.

Cuando l o u no son enteros, Minitab hace una interpolación lineal entre los dos números en cualquiera de los lados de l o de u. La fórmula es:

d_y + z(d_y+1 - d_y)

Por ejemplo, si l = 5.25, el borde inferior es igual a x₅ + 0.25(x₆ - x₅).

Minitab no muestra el intervalo de confianza cuando o .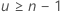

Notación

Término	Description
α	1- nivel de confianza/100
B	número de remuestreos
Xy	la yésima fila de los datos cuando los datos se ordenan de menor a mayor
y	el valor truncado de l o u
z	l-y o u - y