Interpretar los resultados clave para la Remuestreo bootstrap para función de 1 muestra

Complete los siguientes pasos para interpretar un análisis de procedimiento bootstrap de función de 1 muestra. La salida clave incluye el histograma, la estimación del parámetro y el intervalo de confianza.

En este tema

Paso 1: Examinar la forma de la distribución bootstrap
Paso 2: Determinar un intervalo de confianza para el parámetro de la población

Paso 1: Examinar la forma de la distribución bootstrap

Utilice el histograma para examinar la forma de la distribución bootstrap. La distribución bootstrap es la distribución del estadístico elegido de cada muestra repetida. La distribución bootstrap debe parecer normal. Si la distribución bootstrap es no normal, usted no puede confiar en los resultados bootstrap.

La distribución suele ser más fácil de determinar con más muestras repetidas. Por ejemplo, en estos datos, la distribución es ambigua para 50 muestras repetidas. Con 1000 muestras repetidas, la forma parece aproximadamente normal.

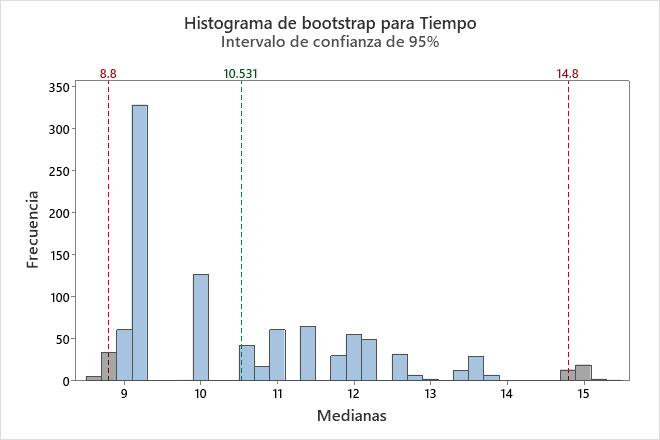
En este histograma, la distribución bootstrap parece ser normal. La muestra original solo tiene 16 puntos de datos. Para obtener un intervalo de confianza fiable, usted debe recopilar una muestra más grande y realizar el análisis nuevamente.

Paso 2: Determinar un intervalo de confianza para el parámetro de la población

Primero, considere el estadístico de la muestra bootstrap y luego examine el intervalo de confianza.

El estadístico de la muestra bootstrap es una estimación del parámetro de la población. Puesto que el estadístico se basa en los datos de una muestra y no en toda la población, es improbable que el estadístico de la muestra sea igual al parámetro de la población. Para estimar mejor el parámetro de la población, utilice el intervalo de confianza.

Los intervalos de confianza se basan en la distribución de muestreo de un estadístico. Si un estadístico no tiene sesgo como estimador de un parámetro, su distribución de muestreo se centra en el valor verdadero del parámetro. Una distribución bootstrap se aproxima a la distribución de muestreo del estadístico. Por lo tanto, el 95% intermedio de los valores de la distribución bootstrap proporciona un intervalo de confianza de 95% para el parámetro. El intervalo de confianza ayuda a evaluar la significancia práctica de la estimación del parámetro de la población. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación.

Nota

Minitab no calcula el intervalo de confianza cuando el número de muestras repetidas es demasiado bajo para obtener un intervalo de confianza preciso.

Muestra observada

Variable	N	Media	Desv.Est.	Varianza	Suma	Mínimo	Mediana	Máximo
Tiempo	16	11.331	3.115	9.702	181.300	7.700	10.050	16.000

Muestras de bootstrap para la media

Número de remuestreos	Media	Desv.Est.	IC de 95% para μ
1000	11.3095	0.7625	(9.8562, 12.8562)

Resultados clave: Promedio, intervalo de confianza de 95%

En estos resultados, la estimación de la diferencia de población es aproximadamente 11.3. Usted puede estar 95% seguro de que la media de población está entre aproximadamente 9,9 y 12,9.