En este tema
- Función de distribución acumulada
- Probabilidad acumulada inversa
- Función de densidad de probabilidad
- Distribución beta
- Distribución binomial
- Distribución de Cauchy
- Distribución de chi-cuadrada
- Distribución discreta
- Distribución exponencial
- Distribución F
- Distribución gamma
- Distribución geométrica
- Distribución hipergeométrica
- Distribución de enteros
- Distribución de Laplace
- Distribución de valor extremo más grande
- Distribución logística
- Distribución loglogística
- Distribución lognormal
- Distribución binomial negativa
- Distribución normal
- Distribución de Poisson
- Distribución de valor extremo más pequeño
- distribución t
- Distribución triangular
- Distribución uniforme
- Distribución de Weibull
Función de distribución acumulada
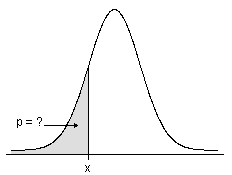
- Para distribuciones continuas, la CDF proporciona el área por debajo de la función de densidad de probabilidad, hasta el valor de x que usted especifique.
- Para distribuciones discretas, la CDF proporciona la probabilidad acumulada para los valores de x que usted especifique.
Probabilidad acumulada inversa
Para un número p en el intervalo cerrado [0,1], la función de distribución acumulada inversa (ICDF) de una variable X aleatoria determina, donde sea posible, un valor de x tal que la probabilidad de X ≤ x sea mayor que o igual a p.
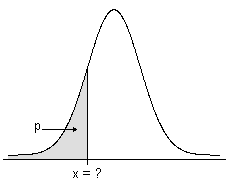
- La ICDF de distribuciones continuas
-
La ICDF es el valor que se asocia con un área por debajo de la función de densidad de probabilidad. La ICDF es la inversa de la función de distribución acumulada (CDF), que es el área que se asocia con un valor.
Para todas las distribuciones continuas, la ICDF existe y es única si 0 < p < 1.
- Cuando la función de densidad de probabilidad (PDF) es positiva para toda la línea de números reales (por ejemplo, la PDF normal), la ICDF no se define para p = 0 ni p = 1.
- Cuando la PDF es positiva para todos los valores que son mayores que cierto valor (por ejemplo, la PDF de chi-cuadrada), la ICDF se define para p = 0, pero no para p = 1.
- Cuando la PDF es positiva solo en un intervalo (por ejemplo, la PDF uniforme), la ICDF se define para p = 0 y p = 1.
- Cuando la ICDF no está definida, Minitab devuelve un valor faltante (*) en el resultado.
- La ICDF para distribuciones discretas
- La ICDF es más complicada para las distribuciones discretas que para las distribuciones continuas. Cuando usted calcula la CDF para una binomial con, por ejemplo, n = 5 y p = 0,4, no hay un valor de x tal que la CDF sea 0,5. Para x = 1, la CDF es 0,3370. Para x = 2, la CDF aumenta a 0,6826.
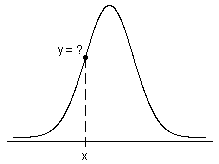
Función de densidad de probabilidad
- Para las distribuciones continuas, la probabilidad de que X tenga valores en un intervalo (a, b) es precisamente el área por debajo de su PDF en el intervalo (a, b).
- Para las distribuciones discretas, la probabilidad de que X tenga valores en un intervalo (a, b) es exactamente la suma de la PDF (también denominada función de masa de probabilidad) de los posibles valores discretos de X en (a, b).
Distribución beta
La distribución beta suele utilizarse para representar procesos con límites inferiores y superiores naturales.
Fórmula
La función de densidad de probabilidad (PDF) es:

Notación
| Término | Description |
|---|---|
| α | parámetro de forma 1 |
| β | parámetro de forma 2 |
| Γ | función gamma |
| a | límite inferior |
| b | límite superior |
Cuando a = 0, b = 1,
la PDF es:
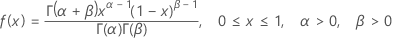


Distribución binomial
La distribución binomial se utiliza para representar el número de eventos que ocurren en n ensayos independientes. Los valores posibles son enteros de cero a n.
Fórmula
media = np
varianza = np(1 – p)
La función de masa de probabilidad (PMF) es:
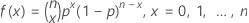
Donde  es igual a
es igual a  .
.
Generalmente, puede calcular k! como 
Notación
| Término | Description |
|---|---|
| n | número de ensayos |
| x | número de eventos |
| p | probabilidad del evento |
Distribución de Cauchy
La distribución de Cauchy es simétrica alrededor de cero, pero las colas se aproximan a cero con menor rapidez que las de la distribución normal.
Fórmula
La función de densidad de probabilidad (PDF) es:
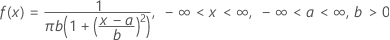
Notación
| Término | Description |
|---|---|
| a | parámetro de ubicación |
| b | parámetro de escala |
| π | Pi (~3.142) |
Nota
Si usted no especifica valores, Minitab utiliza a = 0 y b = 1.
Distribución de chi-cuadrada
Si X tiene una distribución normal estándar, X2 tiene una distribución de chi-cuadrada con un grado de libertad, lo que le permite ser una distribución de muestreo de uso común.
La suma de n variables X2 independientes (donde X tiene una distribución normal estándar) tiene una distribución de chi-cuadrada con n grados de libertad. La forma de la distribución de chi-cuadrada depende del número de grados de libertad.
Fórmula
La función de densidad de probabilidad (PDF) es:
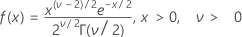
media = v
varianza = 2v
Notación
| Término | Description |
|---|---|
| ν | grados de libertad |
| Γ | función gamma |
| e | base del logaritmo natural |
Distribución discreta
Una distribución discreta es una distribución que usted mismo define. Por ejemplo, supongamos que usted está interesado en una distribución compuesta por tres valores −1, 0, 1, con probabilidades de 0.2, 0.5 y 0.3, respectivamente. Si ingresa los valores en columnas de una hoja de trabajo, entonces puede utilizar estas columnas para generar datos aleatorios o calcular probabilidades.
| Valor | Prob |
|---|---|
| −1 | 0.2 |
| 0 | 0.5 |
| 1 | 0.3 |
Distribución exponencial
La distribución exponencial se puede utilizar para modelar tiempo entre fallas, como cuando las unidades tienen una tasa de fallas constante e instantánea (función de riesgo). La distribución exponencial es un caso especial de la distribución de Weibull y la distribución gamma.
Fórmula
La función de densidad de probabilidad (PDF) es:
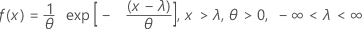
La función de distribución acumulada (CDF) es:

media = θ + λ
varianza = θ2
Notación
| Término | Description |
|---|---|
| θ | parámetro de escala |
| λ | parámetro de valor umbral |
| exp | base del logaritmo natural |
Nota
Algunas referencias utilizan 1 / θ para un parámetro.
Distribución F
La distribución F también es conocida como la distribución de relación de varianzas y tiene dos tipos de grados de libertad: grados de libertad del numerador y grados de libertad del denominador. Es la distribución de la relación de dos variables aleatorias independientes con distribuciones de chi-cuadrada, cada una de las cuales se divide entre sus grados de libertad.
Fórmula
La función de densidad de probabilidad (PDF) es:
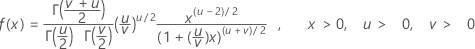

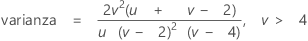
Notación
| Término | Description |
|---|---|
| Γ | función gamma |
| u | grados de libertad del numerador |
| v | grados de libertad del denominador |
Distribución gamma
La distribución gamma se utiliza comúnmente para modelar datos asimétricos positivamente.
Fórmula
La función de densidad de probabilidad (PDF) es:

media = ab + θ
varianza = ab2
Notación
| Término | Description |
|---|---|
| a | parámetro de forma (cuando a = 1, la PDF de gamma es la misma que la PDF exponencial) |
| b | parámetro de escala |
| θ | parámetro de valor umbral |
| Γ | función gamma |
| e | base del logaritmo natural |
Nota
Algunas referencias utilizan 1 / b para un parámetro.
Distribución geométrica
La distribución geométrica discreta se aplica a una secuencia de experimentos de Bernoulli independientes con un evento de interés que tiene una probabilidad p.
Fórmula
Si la variable aleatoria X es el número total de ensayos necesarios para producir un evento con probabilidad p, entonces la función de masa de probabilidad (PMF) de X viene dada por:

y X presenta las siguientes propiedades:

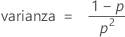
Si la variable aleatoria Y es el número de no eventos que ocurren antes de que se observe el primer evento (con probabilidad p), entonces la función de masa de probabilidad (PMF) de Y viene dada por:

y Y presenta las siguientes propiedades:

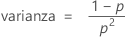
Notación
| Término | Description |
|---|---|
| X | número de ensayos para producir un evento, Y + 1 |
| Y | número de no eventos que ocurren antes del primer evento |
| p | probabilidad de que ocurra un evento en cada ensayo |
Distribución hipergeométrica
La distribución hipergeométrica se utiliza para muestras obtenidas de poblaciones pequeñas, sin reemplazo. Por ejemplo, usted tiene un envío de N televisores, donde N1 se encuentran en buen estado (éxito) y N2 están defectuosos (falla). Si usted toma una muestra de n televisores de N aleatoriamente, sin reemplazo, puede determinar la probabilidad de que exactamente x de los n televisores estén en buen estado.
Fórmula
La función de masa de probabilidad (PMF) es:
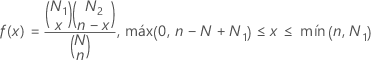

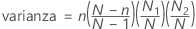
Notación
| Término | Description |
|---|---|
| N | N1 + N2 = tamaño de la población |
| N1 | número de eventos en la población |
| N2 | número de no eventos en la población |
| n | tamaño de la muestra |
| x | número de eventos en la muestra |
Distribución de enteros
La distribución de enteros es una distribución uniforme discreta en un conjunto de enteros. Cada entero tiene igual probabilidad de ocurrir.
Distribución de Laplace
La distribución de Laplace se utiliza cuando la distribución tiene un pico más alto que una distribución normal.
Fórmula
La función de densidad de probabilidad (PDF) es:
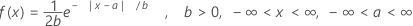
media = a
varianza = 2b2
Notación
| Término | Description |
|---|---|
| a | parámetro de ubicación |
| b | parámetro de escala |
| e | base del logaritmo natural |
Distribución de valor extremo más grande
Utilice la distribución de valor extremo más grande para modelar el valor más grande de una distribución. Si usted tiene una secuencia de distribuciones exponenciales y X(n) es el máximo de la primera n, entonces X(n) – ln(n) converge en distribución a la distribución de valor extremo más grande. Por lo tanto, para valores grandes de n, la distribución de valor extremo más grande es una aproximación adecuada a la distribución de X(n) – ln(n).
Fórmula
La función de densidad de probabilidad (PDF) es:

La función de distribución acumulada (CDF) es:

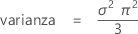
media = μ + γσ
varianza = π 2 σ 2 / 6
Notación
| Término | Description |
|---|---|
| σ | parámetro de escala |
| μ | parámetro de ubicación |
| γ | Constante de Euler (~0.57722) |
Distribución logística
Una distribución continua que es simétrica, similar a la distribución normal, pero con colas más pesadas.
Fórmula
La función de densidad de probabilidad (PDF) es:
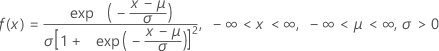
La función de distribución acumulada (CDF) es:
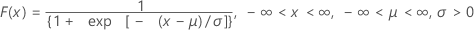
media = μ
Notación
| Término | Description |
|---|---|
| μ | parámetro de ubicación |
| σ | parámetro de escala |
Distribución loglogística
Una variable x tiene una distribución loglogística con valor umbral λ si Y = log (x – λ) tiene una distribución loglogística.
Fórmula
La función de densidad de probabilidad (PDF) es:
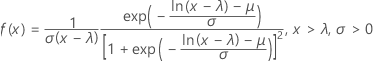
La función de distribución acumulada (CDF) es:

cuando σ < 1:

cuando σ < 1/2:
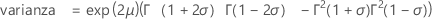
Notación
| Término | Description |
|---|---|
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| λ | parámetro de valor umbral |
| Γ | función gamma |
| exp | base del logaritmo natural |
Distribución lognormal
Una variable x tiene una distribución lognormal si log(x – λ ) tiene una distribución normal.
Fórmula
La función de densidad de probabilidad (PDF) es:

La función de distribución acumulada (CDF) es:



Notación
| Término | Description |
|---|---|
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| λ | parámetro de valor umbral |
| π | Pi (~3.142) |
Distribución binomial negativa
La distribución binomial negativa discreta se aplica a una serie de experimentos de Bernoulli independientes con un evento de interés que tiene una probabilidad p.
Fórmula


Si la variable aleatoria Y es el número de no eventos que ocurren antes de que usted observe los eventos r, cada uno con una probabilidad p, entonces la función de masa de probabilidad (PMF) de Y viene dada por:
y Y presenta las siguientes propiedades:

Nota
Esta distribución binomial negativa también se conoce como la distribución de Pascal.
Notación
| Término | Description |
|---|---|
| X | Y + r |
| r | número de eventos |
| p | probabilidad de un evento |
Distribución normal
La distribución normal (también conocida como distribución de Gauss) es la distribución estadística más utilizada debido a los muchos procesos físicos, biológicos y sociales que puede modelar.
Fórmula
La función de densidad de probabilidad (PDF) es:
La función de distribución acumulada (CDF) es:
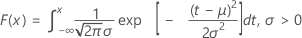
media = μ
varianza = σ 2
desviación estándar = σ
Notación
| Término | Description |
|---|---|
| exp | base del logaritmo natural |
| π | Pi (~3.142) |
Distribución de Poisson
La distribución de Poisson es una distribución discreta que modela el número de eventos con base en una tasa constante de ocurrencia. La distribución de Poisson se puede utilizar como una aproximación a la binomial cuando el número de ensayos independientes sea grande y la probabilidad de éxito sea pequeña.
Fórmula
La función de masa de probabilidad (PMF) es:
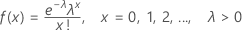
media = λ
varianza = λ
Notación
| Término | Description |
|---|---|
| e | base del logaritmo natural |
Distribución de valor extremo más pequeño
Utilice la distribución de valor extremo más pequeño para modelar el valor más pequeño de una distribución. Si Y sigue una distribución de Weibull, entonces log(Y) sigue una distribución de valor extremo más pequeño.
Fórmula
La función de densidad de probabilidad (PDF) es:
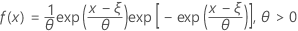
La función de distribución acumulada (CDF) es:



Notación
| Término | Description |
|---|---|
| ξ | parámetro de ubicación |
| θ | parámetro de escala |
| e | base del logaritmo natural |
| v | Constante de Euler (~0.57722) |
distribución t
- Crear intervalos de confianza de la media de la población de una distribución normal cuando se desconoce la varianza.
- Determinar si las medias de dos muestras de poblaciones normales con varianzas desconocidas, aunque iguales, son significativamente diferentes.
- Probar la significancia de los coeficientes de regresión.
Fórmula
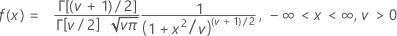
media = 0, cuando ν > 0

Notación
| Término | Description |
|---|---|
| Γ | función gamma |
| v | grados de libertad |
| π | Pi (~3.142) |
Distribución triangular
La PDF de la distribución triangular tiene una forma triangular.
Fórmula
La función de densidad de probabilidad (PDF) es:
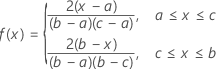
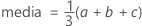
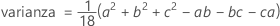
Notación
| Término | Description |
|---|---|
| a | cota inferior |
| b | cota superior |
| c | moda (ubicación donde la PDF alcanza su pico) |
Distribución uniforme
La distribución uniforme caracteriza los datos en un intervalo de manera uniforme, siendo a el valor más pequeño y b el valor más grande.
Fórmula
La función de densidad de probabilidad (PDF) es:



Notación
| Término | Description |
|---|---|
| a | cota inferior |
| b | cota superior |
Distribución de Weibull
La distribución de Weibull es útil para modelar tiempos de falla de los productos.
Fórmula
La función de densidad de probabilidad (PDF) es:
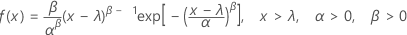
La función de distribución acumulada (CDF) es:


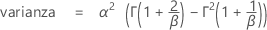
Notación
| Término | Description |
|---|---|
| α | parámetro de escala |
| β | parámetro de forma, cuando β = 1, la PDF de Weibull es igual a la PDF exponencial |
| λ | parámetro de valor umbral |
| Γ | función gamma |
| exp | base del logaritmo natural |
Nota
Algunas referencias utilizan 1/α como un parámetro.
