Paso 1: Evaluar las características clave
Examine el centro de la distribución. Evalúe cómo el tamaño de la muestra puede afectar la apariencia de la gráfica de intervalo.
Centro
- Intervalo de confianza
- El intervalo de confianza es un rango de valores que probablemente incluya la media de la población.
- Media de la muestra
- La media de la muestra es representada por un símbolo.

Investigue los intervalos de confianza que le sorprendan o que no esperaba. Por ejemplo, si un intervalo de confianza para la media de una muestra de los tiempos de espera de un cliente es sustancialmente diferente de los intervalos de confianza de las muestras anteriores, usted debería intentar determinar la causa de la diferencia.
Tamaño de la muestra (n)
El tamaño de la muestra puede afectar la apariencia de la gráfica.
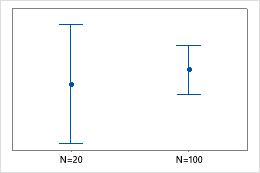
Generalmente, mientras más grande es el tamaño de muestra, más pequeño y más preciso es el intervalo de confianza. Si el intervalo de confianza es demasiado amplio, trate de recopilar una muestra más grande. Las diferencias grandes en los tamaños de las muestras entre grupos (o múltiples variables Y) pueden afectar los anchos de los intervalos y producir resultados engañosos. Si los tamaños de las muestras de los grupos (o múltiples variables Y) son aproximadamente iguales, usted puede estar más seguro de que las diferencias en los anchos de los intervalos se debe principalmente a diferencias en la variación.
Paso 2: Evaluar y comparar los grupos
Si su gráfica de intervalo tiene grupos, evalúe y compare el centro y la dispersión de los grupos.
Centros
Determine si los intervalos de confianza se sobreponen. Si los intervalos de dos medias no se sobreponen, las medias de la población pueden ser estadísticamente significativas.
Por ejemplo, en la primera gráfica de intervalo, los intervalos primero y segundo se sobreponen, pero no sobreponen el tercer intervalo. Por lo tanto, la media del tercer grupo podría ser significativamente diferente de las medias de los otros dos grupos. En la segunda gráfica de intervalo, los intervalos no se sobreponen. Por lo tanto, las diferencias en las medias podrían ser estadísticamente significativas.
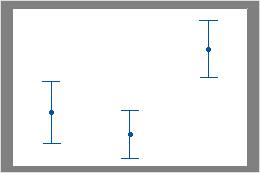
Algunos intervalos se sobreponen
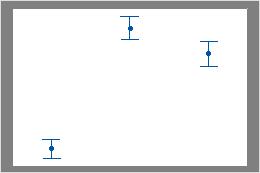
Ningún intervalo se sobrepone
- Utilice una prueba t de 2 muestras si solamente tiene dos grupos.
- Utilice una ANOVA de un solo factor si tiene tres o más grupos.
Dispersiones
Buscar diferencias entre las dispersiones de los grupos.
Los intervalos de esta gráfica tienen centros similares, pero dispersiones diferentes.
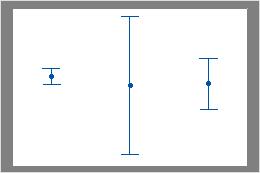
Sugerencia
Para determinar si una diferencia en el ancho de un intervalo obedece a una diferencia en la variación de una muestra o a una diferencia en el tamaño de la muestra, haga doble clic en un intervalo. En la ficha Opciones, haga clic en Agrupar error entre los grupos. Esta acción recrea los intervalos utilizando la desviación estándar agrupada, en lugar de las desviaciones estándar individuales. Cualquier diferencia en los anchos que observe ahora se deben únicamente a tamaños de muestra diferentes.
- Utilice una prueba de 2 varianzas si solamente tiene dos grupos.
- Utilice una prueba de igualdad de varianzas si tiene tres o más grupos.
