Distribución exponencial
Utilice la distribución exponencial para modelar el tiempo entre eventos en un proceso continuo de Poisson. Se presupone que eventos independientes ocurren a una tasa constante.
Esta distribución tiene una amplia gama de aplicaciones, que incluyen el análisis de fiabilidad de productos y sistemas, teorías de colas y cadenas de Markov.
- Cuánto tiempo tarda en fallar un componente electrónico
- El intervalo de tiempo entre las llegadas de clientes a una terminal
- El tiempo que esperan los clientes en fila hasta recibir servicio
- El tiempo hasta que se declara el incumplimiento de un pago (modelos de riesgo de crédito).
- El tiempo para desintegración de un núcleo radiactivo
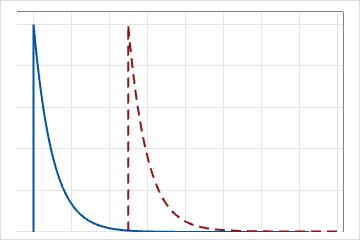
Para la distribución exponencial de 1 parámetro, el valor umbral es cero y la distribución se define por su parámetro de escala. Para la distribución exponencial de 1 parámetro, el parámetro de escala es igual a la media.
¿Qué significa "sin memoria"?
Una propiedad importante de la distribución exponencial es que no tiene memoria. La probabilidad de un evento no depende de los ensayos anteriores. Por lo tanto, la tasa de ocurrencia se mantiene constante.
La propiedad de ausencia de memoria indica que la vida útil restante de un componente no depende de su antigüedad actual. Por ejemplo, ensayos aleatorios de lanzamientos al aire de una moneda demuestran la propiedad de ausencia de memoria. Un sistema que experimenta un desgaste natural y, por lo tanto, tiene más probabilidades de fallar más tarde en su vida útil no es un sistema sin memoria.
Distribución gamma
Utilice la distribución gamma para modelar valores de datos positivos que sean asimétricos a la derecha y mayores que 0. La distribución gamma se utiliza comúnmente en estudios de supervivencia para determinar la fiabilidad. Por ejemplo, la distribución gamma puede describir el tiempo que transcurre para que falle un componente eléctrico. La mayoría de los componentes eléctricos de un tipo particular fallará aproximadamente en el mismo momento, pero unos pocos tardarán más en fallar.
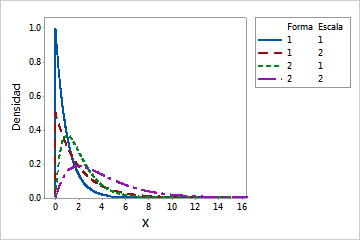
Cuando el parámetro de forma es un entero, la distribución gamma a veces se menciona como distribución de Erlang. La distribución de Erlang se utiliza frecuentemente en aplicaciones de teorías de colas.
Distribución logística
Utilice la distribución logística para modelar distribuciones de datos que tengan colas más grandes y curtosis más alta que la distribución normal.
- Efecto del parámetro de escala
- La siguiente gráfica muestra el efecto de los diferentes valores del parámetro de escala en la distribución logística.
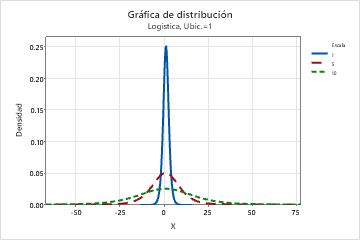
- Efecto del parámetro de ubicación
- La siguiente gráfica muestra el efecto de los diferentes valores del parámetro de ubicación en la distribución logística.
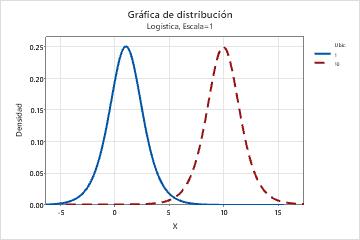
Distribución loglogística
Utilice la distribución loglogística cuando el logaritmo de la variable esté distribuido logísticamente. Por ejemplo, la distribución loglogística se utiliza en modelos de crecimiento y para modelar respuestas binarias en campos como la bioestadística y la economía.
La distribución loglogística es una distribución continua que se define por sus parámetros de escala y ubicación. La distribución loglogística de 3 parámetros se define por sus parámetros de escala, ubicación y valor umbral.
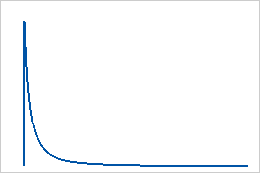
La distribución loglogística también se conoce como distribución de Fisk.
Distribución lognormal
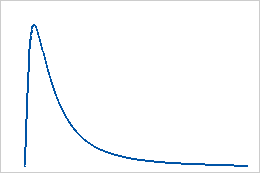
Utilice la distribución lognormal si el logaritmo de la variable aleatoria está distribuida normalmente. Utilícese cuando las variables aleatorias sean mayores que 0. Por ejemplo, la distribución lognormal se usa para el análisis de fiabilidad y en aplicaciones financieras, como modelar el comportamiento de las acciones.
La distribución lognormal es una distribución continua que se define por sus parámetros de ubicación y escala. La distribución lognormal de 3 parámetros se define por sus parámetros de ubicación, escala y valor umbral.
Distribución normal
La distribución normal es una distribución continua que se especifica por la media (μ) y la desviación estándar (σ). La media es el pico o centro de la curva en forma de campana. La desviación estándar determina la dispersión de la distribución.
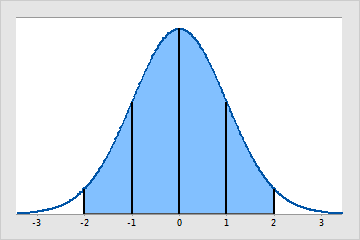
La distribución normal es la distribución estadística más común debido a que la normalidad aproximada ocurre naturalmente en muchas situaciones de mediciones físicas, biológicas y sociales. Muchos análisis estadísticos presuponen que los datos provienen de poblaciones distribuidas normalmente.
Distribuciones de valor extremo más pequeño y más grande
La distribución de valor extremo más grande y la distribución de valor extremo más pequeño están estrechamente relacionadas. Por ejemplo, si X tiene una distribución de valor extremo más grande, entonces −X tiene una distribución de valor extremo más pequeño y viceversa.
Distribución de valor extremo más pequeño
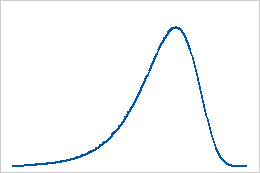
Distribución de valor extremo más grande
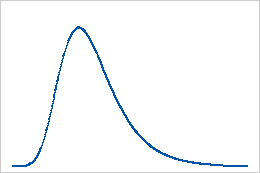
Distribución de Weibull
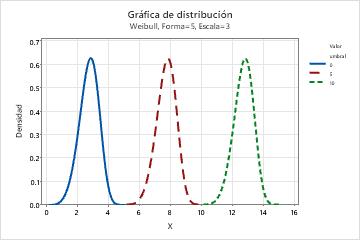
La distribución de Weibull es una distribución versátil que se puede utilizar para modelar una amplia gama de aplicaciones en ingeniería, investigación médica, control de calidad, finanzas y climatología. Por ejemplo, la distribución se utiliza frecuentemente con análisis de fiabilidad para modelar datos de tiempo antes de falla. La distribución de Weibull también se utiliza para modelar datos asimétricos del proceso en el análisis de capacidad.
La distribución de Weibull se describe según los parámetros de forma, escala y valor umbral y también se conoce como la distribución de Weibull de 3 parámetros. El caso en el que el parámetro de valor umbral es cero se conoce como la distribución de Weibull de 2 parámetros. La distribución de Weibull de 2 parámetros se define solo para variables positivas. Una distribución de Weibull de 3 parámetros puede funcionar con ceros y datos negativos, pero todos los datos para una distribución de Weibull de 2 parámetros deben ser mayores que cero.
Dependiendo de los valores de sus parámetros, la distribución de Weibull puede adoptar varias formas.
- Efecto del parámetro de forma
- El parámetro de forma describe la manera en que se distribuyen los datos. Una forma de 3 se aproxima a una curva normal. Un valor de forma bajo, por ejemplo 1, da una curva con asimetría hacia la derecha. Un valor de forma alto, por ejemplo 10, da una curva con asimetría hacia la izquierda.
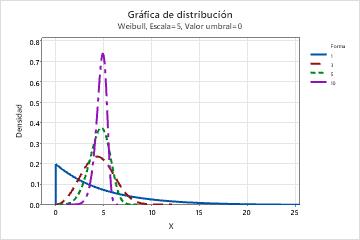
- Efecto del parámetro de escala
- La escala, o vida característica, es el percentil 63.2 de los datos. La escala define la posición de la curva de Weibull respecto del valor umbral, lo cual es similar a la manera en que la media define la posición de una curva normal. Una escala de 20, por ejemplo, indica que el 63.2% de los equipos fallará en las primeras 20 horas después del valor umbral de tiempo.
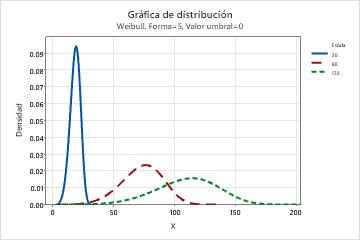
- Efecto del parámetro de valor umbral
- El parámetro de valor umbral describe un desplazamiento de la distribución alejándose del 0. Un valor umbral negativo desplaza la distribución hacia la izquierda, mientras que un valor umbral positivo desplaza la distribución hacia la derecha. Todos los datos deben ser mayores que el valor umbral. La distribución de Weibull de 2 parámetros es igual a la distribución de Weibull de 3 parámetros con un valor umbral de 0. Por ejemplo, la distribución de Weibull de 3 parámetros (3,100,50) tiene la misma forma y dispersión que la distribución de Weibull de 2 parámetros (3.100), pero está desplazada 50 unidades hacia la derecha.