En este tema
Paso 1: Evaluar las características clave
Examine el centro y la dispersión de la distribución. Evalúe cómo el tamaño de la muestra puede afectar la apariencia de la gráfica de caja.
Centro y dispersión
- Mediana
- La mediana está representada por la línea en la caja. La mediana es una medida común del centro de sus datos. La mitad de las observaciones es menor que o igual al valor y la mitad es mayor que o igual al valor.
- Caja de rango intercuartil
- La caja de rango intercuartil representa el 50% intermedio de los datos. Muestra la distancia entre el primer cuartil y el tercer cuartil (Q3-Q1).
- Bigotes
- Los bigotes se extienden de cualquier lado de la caja. Los bigotes representan los rangos del 25 % de valores de datos de la parte inferior y el 25 % de la parte inferior, excluyendo los valores atípicos.
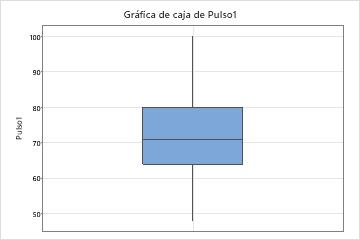
Mantenga el puntero sobre la gráfica de caja para mostrar una sugerencia que muestre estos estadísticos. Por ejemplo, esta gráfica de caja del ritmo cardíaco en reposo muestra que la mediana del ritmo cardíaco es de 71. La mayoría de los sujetos tienen un ritmo cardíaco en reposo que está entre 64 y 80, pero algunos sujetos tienen ritmos cardíacos que son tan bajos como 48 y tan altos como 100.
Investigue cualquier característica sorpresiva o no deseada en la gráfica de caja. Por ejemplo, una gráfica de caja puede mostrar que la longitud mediana de las tablas de madera es mucho más pequeña que la longitud objetivo de 8 pies.
Nota
Dado que los cuartiles de la gráfica de caja son valores calculados, no pueden ser observaciones reales en su conjunto de datos. Para obtener información adicional sobre cómo interpretar los cuartiles, vaya a ¿Qué son cuartiles?. Para obtener información específica sobre cómo se calculan los cuartiles, vaya a Métodos y fórmulas para Resumen gráfico.
Tamaño de la muestra (n)
El tamaño de la muestra puede afectar la apariencia de la gráfica.
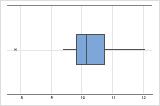
n = 15
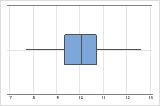
n = 500
Una gráfica de caja funciona mejor cuando el tamaño de la muestra es al menos de 20. Si el tamaño de la muestra es demasiado pequeño, los cuartiles y los valores atípicos que la gráfica de caja muestra pueden no ser significativos. Si el tamaño de la muestra es menor que 20, considere usar en su lugar una Gráfica de valores individuales.
Paso 2: Buscar indicadores de datos inusuales o no normales
Los datos asimétricos indican que los datos podrían ser no normales. Los valores atípicos pueden indicar otras condiciones en sus datos.
Datos asimétricos
Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. La asimetría indica que los datos pueden no estar distribuidos normalmente.
Estas gráficas de caja ilustran los datos asimétricos. La gráfica de caja con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos tiempos de espera son largos. La gráfica de caja con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos más fallan posteriormente.
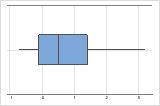
Asimétrico hacia la derecha
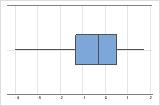
Asimétrico hacia la izquierda
Si usted está en conocimiento de que sus datos no son naturalemente asimétricos, investigue las posibles causas. Si desea analizar los datos marcadamente asimétricos, lea el tema Consideraciones acerca de los datos para el análisis a fin de asegurarse de que pueda utilizar los datos que no sean normales.
Valores atípicos
Los valores atípicos, que son valores de datos que están muy alejados de otros valores de datos, pueden afectar fuertemente sus resultados. Frecuentemente, es más fácil identificar los valores atípicos en una gráfica de caja.
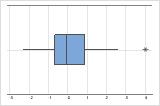
Sugerencia
Mantenga el puntero sobre el valor atípico para identificar el punto de datos.
Intente identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). A continuación, repita el análisis.
Paso 3: Evaluar y comparar los grupos
Si su gráfica de caja tiene grupos, evalúe y compare el centro y la dispersión de los grupos.
Centros
Buscar diferencias entre los centros de los grupos.
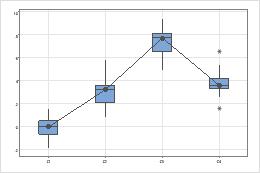
Dispersiones
Buscar diferencias entre las dispersiones de los grupos.
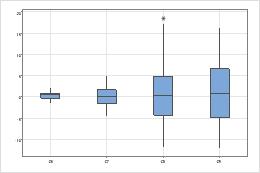
- Utilice una prueba de 2 varianzas si solamente tiene dos grupos.
- Utilice una prueba de igualdad de varianzas si tiene tres o más grupos.
