Suma
La suma es el total de todos los valores de los datos. La suma también se utiliza en cálculos estadísticos, como por ejemplo la media y la desviación estándar.
Media
La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
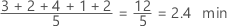
Interpretación
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de la distribución de los datos.
Simétrica
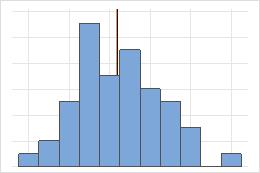
No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
Debido a que la desviación estándar utiliza las mismas unidades que los datos, generalmente es más fácil de interpretar que la varianza.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Un valor de desviación estándar más alto indica una mayor dispersión de los datos. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
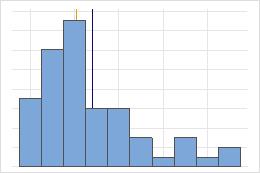
Hospital 1
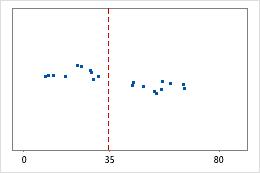
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Mínimo
El mínimo es el valor más pequeño de los datos.
En estos datos, el mínimo es 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el mínimo para identificar un posible valor atípico o un error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor mínimo es muy bajo, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Máximo
El máximo es el valor más grande de los datos.
En estos datos, el máximo es 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el máximo para identificar un posible valor atípico o error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor máximo es muy alto, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Rango
El rango es la diferencia entre los valores más grande y más pequeño de los datos. El rango representa el intervalo que contiene todos los valores de los datos.
Interpretación
Utilice el rango para entender la cantidad de dispersión en los datos. Un valor de rango grande indica mayor dispesión en los datos. Un valor de rango pequeño indica que hay menos dispersión en los datos. Puesto que el rango se calcula usando solo dos valores de los datos, es más útil con conjuntos de datos pequeños.
Mediana
La mediana es el punto medio del conjunto de datos. El valor de este punto medio es el punto en el cual la mitad de las observaciones está por encima del valor y la otra mitad está por debajo del valor. La mediana se determina jerarquizando las observaciones y hallando la observación que ocupe el número [N + 1] / 2 en el orden jerarquizado. Si el número de observaciones es par, entonces la mediana es el valor promedio de las observaciones jerarquizadas en los números N / 2 y [N / 2] + 1.
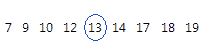
Para estos datos ordenados, la mediana es 13. Es decir, la mitad de los valores es menor que o igual a 13 y la otra mitad de los valores es mayor que o igual a 13. Si usted agrega otra observación igual a 20, la mediana es 13,5, que es el promedio entre la 5ta observación (13) y la 6ta observación (14).
Interpretación

Simétrica

No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
Suma de los cuadrados
La suma de los cuadrados no corregida se calcula elevando al cuadrado cada uno de los valores de la columna y sumando luego esos valores elevados al cuadrado. Por ejemplo, si la columna contiene x1, x2, ... , xn, entonces la suma de los cuadrados calcula (x12 + x22 + ... + xn2). A diferencia de la suma de los cuadrados corregida, la suma de los cuadrados no corregida incluye el error. Los valores de datos se elevan al cuadrado sin antes restar la media.
Conteo total
El número total de observaciones en la columna. Utilícese para representar la suma de N valores faltantes y N valores presentes.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
El número de valores presentes en la muestra.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N*
El número de valores faltantes en la muestra. El número de valores faltantes se refiere a las celdas que contienen el símbolo de valor faltante *.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
