Para utilizar estas funciones, elija .
Las funciones Gamma, Gamma incompleta y Logaritmo natural de gamma amplían la función factorial (1 * 2 * 3...* n) de manera que se pueden calcular factoriales para fracciones, además de números enteros positivos. La función Logaritmo natural de gamma a veces se utiliza en los cálculos en lugar de la función Gamma porque es menos probable que el Logaritmo natural de gamma genere números muy grandes que puedan ser mayores que la capacidad de almacenamiento y causar sobreflujo.
Sintaxis
- GAMMA(forma)
- IGAMMA(límite,forma)
- LNGAMMA(forma)
En forma, especifique el número del que desea obtener la función. En límite, especifique el límite superior de la integral.
Ejemplos
| Expresión de la calculadora | Resultado |
|---|---|
| GAMMA(0.5) | 1.77245 |
| IGAMMA(1,2) | 0.264241 |
| LNGAMMA(3.5) | 1.20097 |
Fórmulas
, también se conoce como función factorial generalizada y se define como:
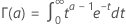
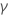, es una variación de la función gamma completa definida por una integral con un límite superior finito, en vez de un límite superior infinito. Para un número dado a y un límite superior x,
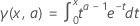
La función Logaritmo natural de gamma, 
, es el logaritmo natural de la función gamma completa.
Nota
La función Gamma completa es indefinida cuando la variable a es igual a un entero negativo o cero. La función Gamma incompleta es indefinida cuando la variable a es igual a cualquier número negativo o cero. Minitab devuelve un valor faltante * cuando la función Gamma de un número es indefinida.
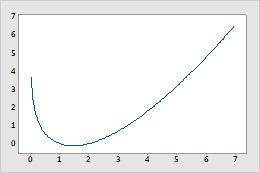
Función Lngamma
El Logaritmo natural de gamma es una función convexa definida solo para números positivos.
Usos
La función Gamma es importante en matemáticas puras y aplicadas, ciencia e ingeniería, incluyendo los usos en los que se debe estudiar la conducción del calor en los rayos láser y tejidos humanos. En estadística, la función Gamma se utiliza para calcular la función de densidad de probabilidad y la función de distribución acumulada de la distribución gamma, las cuales se pueden utilizar para describir datos positivamente asimétricos.
