In This Topic
Step 1: Examine the shape of your bootstrap distribution
50 resamples
1000 resamples
The distribution is usually easier to determine with more resamples. For example, in these data, the distribution is ambiguous for 50 resamples. With 1000 resamples, the shape looks approximately normal.
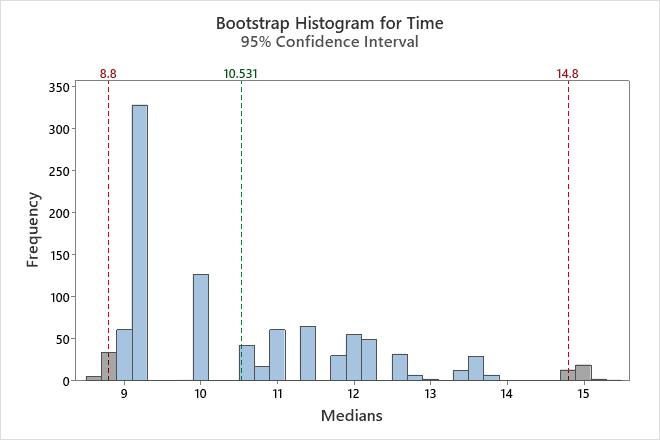
In this histogram, the bootstrap distribution does not appear to be normal. The original sample has only 16 data points. To get a reliable confidence interval, you should collect a larger sample and perform the analysis again.
Step 2: Determine a confidence interval for the population parameter
First, consider the statistic from the bootstrap sample, and then examine the confidence interval.
The statistic of the bootstrap sample is an estimate of the population parameter. Because the statistic is based on sample data and not the entire population, it is unlikely that the sample statistic equals the population parameter. To better estimate the population parameter, use the confidence interval.
Confidence intervals are based on the sampling distribution of a statistic. If a statistic has no bias as an estimator of a parameter, its sampling distribution is centered at the true value of the parameter. A bootstrapping distribution approximates the sampling distribution of the statistic. Therefore, the middle 95% of values from the bootstrapping distribution provide a 95% confidence interval for the parameter. The confidence interval helps you assess the practical significance of your estimate for the population parameter. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation.
Note
Minitab does not calculate the confidence interval when the number of resamples is too small to obtain an accurate confidence interval.
Observed Sample
| Variable | N | Mean | StDev | Variance | Sum | Minimum | Median | Maximum |
|---|---|---|---|---|---|---|---|---|
| Time | 16 | 11.331 | 3.115 | 9.702 | 181.300 | 7.700 | 10.050 | 16.000 |
Bootstrap Samples for Mean
| Number of Resamples | Mean | StDev | 95% CI for μ |
|---|---|---|---|
| 1000 | 11.3095 | 0.7625 | (9.8562, 12.8562) |
Key Results: Average, 95% Confidence Interval
In these results, the estimate for the population mean is approximately 11.3. You can be 95% confident that the population mean is between approximately 9.9 and 12.9.
