A quality engineer at an engine factory wants to perform a test for bimodality on pistons from two suppliers. The engineer measures the lengths of a random sample of 100 pistons from each of the suppliers.
The script uses the diptest package for R to test whether the data are unimodal. If the test rejects the null hypothesis for unimodal data, then the script assumes that the data are a mix of two normal distributions. The script uses the mixtools package for R to display descriptive statistics and density curves for two normal distributions.
- Pass a single column from a Minitab worksheet as input.
- Add a table title.
- Add column labels for a table.
- Send a table to the Minitab Output pane.
- Create a graph and send the graph to the Minitab Output pane.
| File | Description |
|---|---|
| bimodal.R | An R script that takes a column from a Minitab worksheet, tests for unimodality, and produces results for a mix of two normal distributions if the data are not unimodal. |
All the files referenced in this guide are available in this .ZIP file: r_guide_files.zip.
Prerequisites
-
The R script in the below example requires the following R packages:
- mtbr
- The R package that integrates Minitab and R. In the example, functions from this module send R results to Minitab. For information on how to install Minitab's R package, go to Step 2: Install mtbr.
- mixtools
- The R package that the script uses to create output for a mixture of normal distributions.
- diptest
- The R package that the script uses to test whether the data are unimodal.
install.packages("mixtools")For assistance with the installation of R packages, please consult with your organization's technical support department. Minitab Technical Support cannot assist with the installation of R packages.
Steps to run the example
- Ensure you have installed the required modules: mtbr.
- Save the R script file, bimodal.R, to your Minitab default file location. For more information on where Minitab looks for R script files, go to Default folders for R files for Minitab.
- Open the sample data set ProcessEnergyCost.MWX .
-
In the Minitab Command
Line pane, enter
RSCR "bimodal.R" "Process 1". - Select Run.
bimodal.R
# Load the necessary libraries
#Original code by Valentina Tillman
library(mixtools)
library(mtbr)
library(diptest)
# Retrieve sample data
input_column <- commandArgs(trailingOnly = TRUE)
data <- mtb_get_column(input_column)
dip_test_result <- dip.test(data)
if (dip_test_result$p.value < 0.05) {
# Fit a bimodal mixture model
bimodal_fit <- normalmixEM(data, k = 2)
# Manually extract parameter estimates and format them as a data frame
bimodal_table <- data.frame(
Mean = bimodal_fit$mu,
Standard_Deviation = bimodal_fit$sigma,
Proportion = bimodal_fit$lambda #tells you what % of the data is clustered around which mean. Also called lambda
)
# Define title and headers
mytitle <- "Modeling a Bimodal Distribution"
myheaders <- names(bimodal_table)
# Add the table to the mtbr output
mtb_add_table(columns = bimodal_table, headers = myheaders, title = mytitle)
png("r_bimodal_image.png")
plot(bimodal_fit, density = TRUE, which = 2)
graphics.off()
mtb_add_image("r_bimodal_image.png")
# Now generate tolerance intervals using the parameters found using mixtools
# Set the desired coverage level (e.g., 95%)
coverage_level <- 0.95
alpha <- 1 - coverage_level
# Calculate the tolerance intervals for each component
tolerance_intervals <- lapply(1:2, function(i) {
mu <- bimodal_fit$mu[i]
sigma <- bimodal_fit$sigma[i]
n <- bimodal_fit$lambda[i] # proportion of the component
# Calculate the critical value for the normal distribution
z <- qnorm(1 - alpha / (2 * n))
# Calculate lower and upper bounds of the tolerance interval
lower_bound <- mu - z * sigma
upper_bound <- mu + z * sigma
c(lower_bound, upper_bound)
})
# Show the tolerance intervals
tolerance_intervals_df <- data.frame(
Component = c("First Mode", "Second Mode"),
Lower_Bound = sapply(tolerance_intervals, "[", 1),
Upper_Bound = sapply(tolerance_intervals, "[", 2)
)
myheaders <- c("Component", "Lower Bound", "Upper Bound")
mytitle <- "Tolerance Intervals for Bimodal Distribution"
mtb_add_table(columns = tolerance_intervals_df, headers = myheaders, title = mytitle)
} else {
mtb_add_message("This data is unimodal.")
}
Results
Modeling a Bimodal Distribution
| Mean | Standard_Deviation | Proportion |
|---|---|---|
| 34.1875 | 1.50909 | 0.516129 |
| 48.3333 | 1.84992 | 0.483871 |
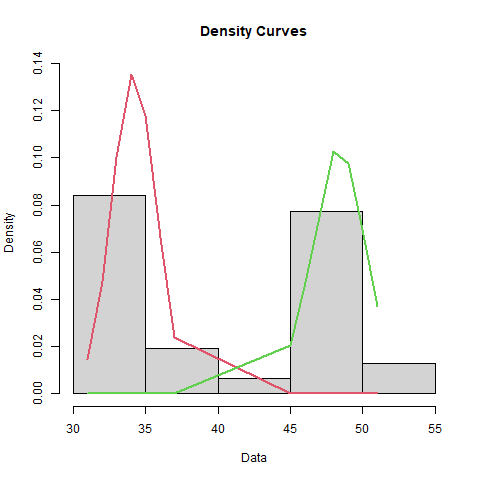
Tolerance Intervals for Bimodal Distribution
| Component | Lower Bound | Upper Bound |
|---|---|---|
| First Mode | 31.6821 | 36.6929 |
| Second Mode | 45.3200 | 51.3467 |
