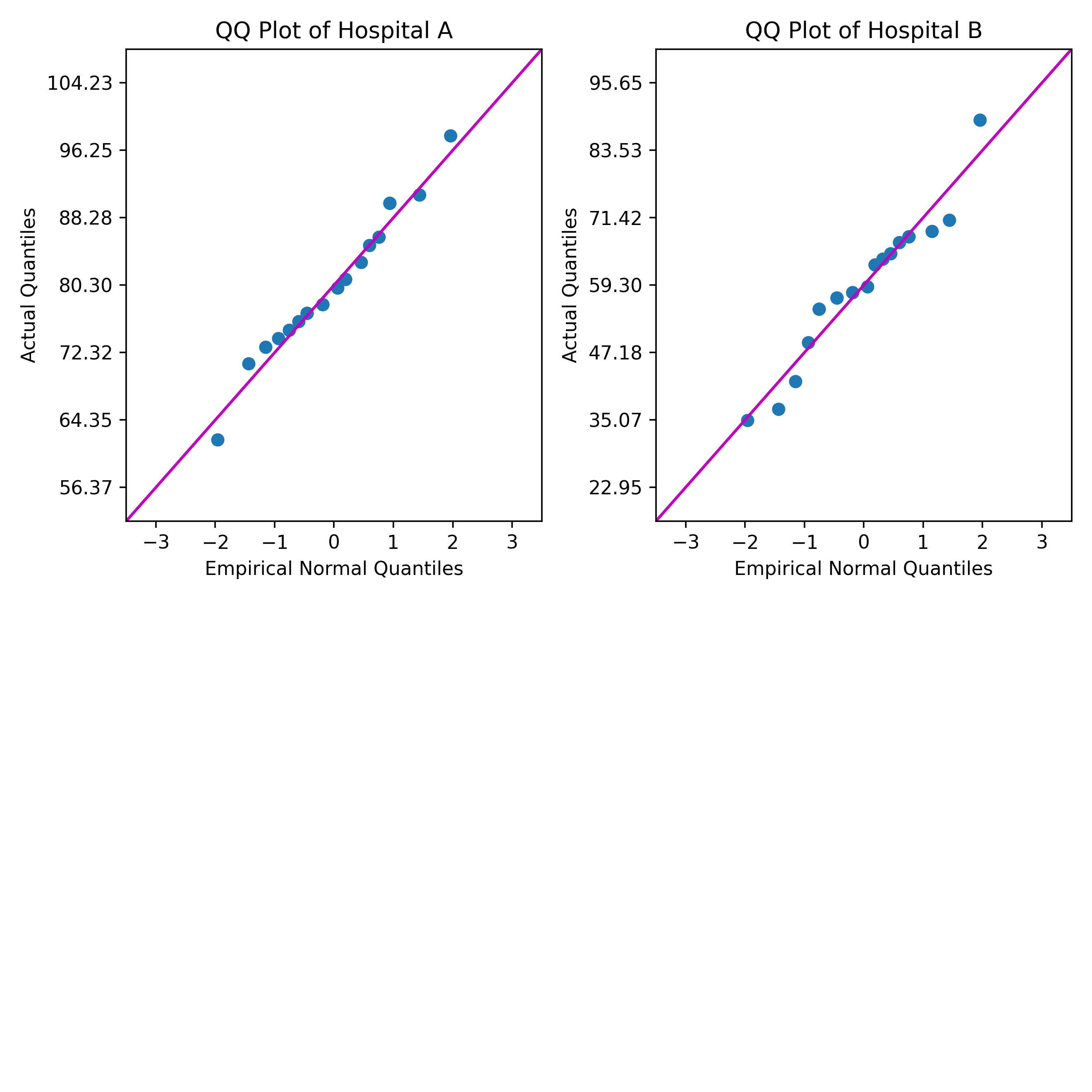
A healthcare consultant wants to compare the normality of patient satisfaction ratings from two hospitals using a quantile-quantile (QQ) plot. QQ plots show how well each set of patient satisfaction ratings fit a normal distribution.
The example Python script reads the data from columns in Minitab Statistical Software. The script calculates the quantiles and creates a QQ plot for each column. Then the script sends the plots to the Minitab Output pane.
All the files referenced in this guide are available in this .ZIP file: python_guide_files.zip.
Use the following files to perform the steps in this section:
| File | Description |
|---|---|
| qq_plot.py | A Python script that takes columns from a Minitab worksheet and displays the QQ Plot for each column. |
The Python script in the below example requires the following
Python modules. The number in parentheses is
the most recent package version that we tested.
- mtbpy
- The Python module that integrates Minitab and Python. In the example, functions from this module send Python results to Minitab.
- numpy (1.24.2)
- A Python module that has various applications for scientific and numerical computing.
- matplotlib (3.7.0)
- A Python module that has various functions related to plotting graphs and creating figures.
- Ensure you have installed the required modules: mtbpy and numpy.
- To install the
required modules via
PIP, run the corresponding command for your
operating system's terminal (for example, the
Microsoft® Windows Command Prompt or the
macOS Terminal):
pip install mtbpy numpy matplotlib
- To install the
required modules via
PIP, run the corresponding command for your
operating system's terminal (for example, the
Microsoft® Windows Command Prompt or the
macOS Terminal):
- Save the Python script file, qq_plot.py, to your Minitab default file location. For more information on where Minitab looks for Python script files, go to Default folders for Python files for Minitab.
- Open the sample data set HospitalComparisonUnstacked.MWX.
-
In the Minitab
Command
Line pane, enter
PYSC "qq_plot.py" "Hospital A" "Hospital B". - Click Run.
qq_plot.py
"""
Description:
_________________________________________________________________________________
This script will generate a QQ Plot for each column of data passed to PYSC.
If PYSC was not given any columns, the script will look for data in every
column starting with the first column (C1) and ending at the first empty column.
The ranks are calculated using the Modified Kaplan-Meier method,
and duplicate values are given the same rank and quantile, this is also known
as "competition" ranking.
_________________________________________________________________________________
Imports:
_________________________________________________________________________________
numbers - For testing the types of the values in the data columns.
sys - For retrieving any columns passed from Minitab.
statistics - For calculating the inverse CDF of the normal distribution.
numpy - For general calculations and manipulating data.
matplotlib - For creating the plots.
mtbpy - For sending and receiving data with Minitab.
_________________________________________________________________________________
"""
import numbers
import sys
from statistics import NormalDist
import numpy as np
from matplotlib import pyplot as plt
from mtbpy import mtbpy
# sys.argv contains the arguments passed to PYSC, with sys.argv[0] being the name of the Python script file,
# and sys.argv[1:] being the list of columns passed after the name of Python script file,
# sys.argv[1:] has a length of 0 if no columns are passed to the PYSC command.
column_names = sys.argv[1:]
# If column_names is empty, loop over each column, starting at C1, and check if they contain data.
# Stop at the first column that does not contain data, and use the range of columns before that column.
if len(column_names) == 0:
i = 1
while mtbpy.mtb_instance().get_column(f"C{i}") is not None:
column_names.append(f"C{i}")
i += 1
# If there are no columns to analyze, throw an error stating that columns need to be passed or the data needs to start in C1
if len(column_names) == 0 or mtbpy.mtb_instance().get_column(column_names[0]) is None:
raise IndexError("Worksheet is empty or column data could not be found!\n\tPass columns to PYSC or move first column to C1.")
# Initialize a list to store data from columns in a list of lists.
columns_data = []
# Loop through each column name.
for column_name in column_names:
# Use mtbpy to get the data from Minitab for the column as a Python list.
column_data = mtbpy.mtb_instance().get_column(column_name)
# If any value in the data is not numeric, throw an error stating that only numeric columns can be used.
if not all(isinstance(value, numbers.Number) for value in column_data):
raise ValueError("Data is not numeric!\n\tPass only numeric columns to PYSC or delete non-numeric columns.")
# Sort the data for calculation of quantiles.
sorted_column_data = np.sort(column_data)
# Append the sorted data to our list of column data.
columns_data.append(sorted_column_data)
# Initialize a figure with:
# Figure Columns = 2 plus the number of data columns modulo 2.
# Figure Rows = Number of data columns floor-divided by the number of figure columns plus 1.
num_plot_cols = 2 + len(columns_data) % 2
num_plot_rows = len(columns_data) // num_plot_cols + 1
fig = plt.figure(figsize=(num_plot_cols * 4, num_plot_rows * 4), tight_layout=True)
# Iterate over the columns and generate a QQ Plot for each column.
for index, column_data in enumerate(columns_data):
# Create an axis on the figure.
current_axis = fig.add_subplot(num_plot_rows, num_plot_cols, index + 1)
# Calculate the quantile of each data point in the column.
# This uses the Modified Kaplan-Meier ranks, however, the ranks produced by
# the numpy.searchsorted method begin at "0" and not "1," which would result
# in negative rank values when using the Modified Kaplan-Meier method.
# Therefore, the calculation uses rank + 1.0 - 0.5, which simplifies to rank + 0.5.
column_ranks = np.searchsorted(np.sort(column_data), column_data) + 0.5
# The quantiles are the ranks divided by the count.
quantiles = column_ranks / len(column_data)
# The tick marks on the y-axis and the fit line use the sample mean and sample standard deviation.
column_mean = np.mean(column_data)
column_stdev = np.std(column_data)
# Calculate the empirical quantiles from the normal distribution.
empirical_quantiles = [NormalDist().inv_cdf(x) for x in quantiles]
# Create a scatterplot of the sample data versus the empirical quantiles.
current_axis.scatter(empirical_quantiles, column_data)
# Create a fit line for a perfect empirical normal distribution, for the scale of this plot, the fit line is 45 degrees.
current_axis.plot([-3.5, 3.5], [column_mean-3.5*column_stdev, column_mean+3.5*column_stdev], "-m")
# Set the title for the plot.
current_axis.set_title(f"QQ Plot of {column_names[index]}")
# Set the x axis label, bounds, and tick mark positions.
current_axis.set_xlabel("Empirical Normal Quantiles")
current_axis.set_xbound(lower=-3.5, upper=3.5)
current_axis.set_xticks([-3, -2, -1, 0, 1, 2, 3])
# Set the y axis label, bounds, and tick mark positions.
current_axis.set_ylabel("Actual Quantiles")
current_axis.set_ybound(lower=column_mean-3.5*column_stdev,
upper=column_mean+3.5*column_stdev)
current_axis.set_yticks([column_mean-3*column_stdev,
column_mean-2*column_stdev,
column_mean-1*column_stdev,
column_mean,
column_mean+1*column_stdev,
column_mean+2*column_stdev,
column_mean+3*column_stdev])
# Save the combined plots figure as a PNG file.
fig.savefig("qqplot.png", dpi=330)
# Send the figure to Minitab.
mtbpy.mtb_instance().add_image("qqplot.png")
Results
Python Script