A quality engineer plans a designed experiment to study the transparency of a plastic part. Before conducting the experiment, the engineer wants to ensure that the experiment will have adequate power. The engineer plans to examine 10 numeric factors. For a base design, the engineer selects a design with 12 experimental runs and 3 center points. The engineer wants to be able to detect an effect of 5 transparency units with no more than 4 replicates. Previous experimentation indicates that 4.5 is an adequate estimate of the standard deviation. The engineer decides to calculate the power for a model with main effects and a term for center points.
- Choose .
- In Number of factors, enter 10.
- In Number of corner points, select 12.
- In Replicates, enter 1 2 3 4.
- In Effects, enter 5.
- In Number of center points, enter 3.
- In Standard deviation, enter 4.5.
- Click OK.
Interpret the results
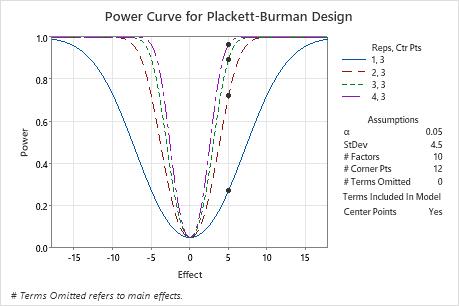
The unreplicated design has a power of approximately 30%. With 3 replicates and 39 total runs, the design has nearly a 90% chance to detect an important effect. With 4 replicates and 51 total runs, the design has more than a 95% chance to detect an important effect. The power curve shows the relationship between power and effect size. The symbols on the curves represent the effect size of 5 that the engineer specified. The engineer decides that the 3 replicate design provides enough power.
Method
| Factors: | 10 | Design: | 12 |
|---|---|---|---|
| Center pts (total): | 3 |
Results
| Center Points | Effect | Reps | Total Runs | Power |
|---|---|---|---|---|
| 3 | 5 | 1 | 15 | 0.272032 |
| 3 | 5 | 2 | 27 | 0.720550 |
| 3 | 5 | 3 | 39 | 0.894838 |
| 3 | 5 | 4 | 51 | 0.963485 |
