Common notation
All of the calculations for the equivalence test for 2x2 crossover design assume that the treatment order for sequence 1 is the reference treatment followed by the test treatment, and that the order for sequence 2 is the test treatment followed by the reference treatment.
Let Yijk be the response for participant k during period j in sequence i, where i = 1, 2; j = 1, 2; k = 1 ... ni .
If the response for either period is missing for a participant, then the data for that participant is omitted from the calculations.
Let d1k and d2k be defined as follows:
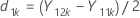
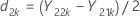
 and S1 represent the sample mean and the sample standard deviation of d1k, k = 1, ..., n1, given by the following:
and S1 represent the sample mean and the sample standard deviation of d1k, k = 1, ..., n1, given by the following:
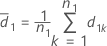
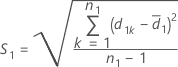
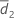 and S2 represent the sample mean and the sample standard deviation of d2k, k = 1, ..., n2 , given by the following:
and S2 represent the sample mean and the sample standard deviation of d2k, k = 1, ..., n2 , given by the following:
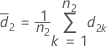
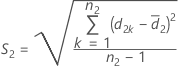
Notation
| Term | Description |
|---|---|
 | Sample mean of d1k, k = 1, ..., n1 |
| S1 | Sample standard deviation of d1k, k = 1, ..., n1 |
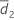 | Sample mean of d2k, k = 1, ..., n2 |
| S2 | Sample standard deviation of d2k, k = 1, ..., n2 |
Degrees of freedom (DF)

Notation
| Term | Description |
|---|---|
| ν | Degrees of freedom |
| n1 | Number of participants in sequence 1 |
| n2 | Number of participants in sequence 2 |
Equivalence limits
Let k1 be the lower limit that you specify andk2 be the upper limit that you specify. By default, the lower equivalence limit, δ1, is given by:

and the upper equivalence limit, δ2, is given by:
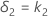
However, if you select the option to multiply your limits by the reference mean,  , then the limits are given by:
, then the limits are given by:


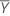 is the average of the average responses for the two reference periods.
is the average of the average responses for the two reference periods.
