Methods and formulas for 1-Sample Equivalence Test

In This Topic

Difference
Standard error of the difference (SE)
Equivalence limits
Degrees of freedom (DF)
Confidence interval for the difference
T-values
P-values

Difference

Notation

Term	Description
D	Difference
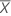	Test mean

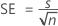
Standard error of the difference (SE)

Notation

Term	Description
s	Standard deviation of the observations
n	Number of observations

Equivalence limits

Let k₁and k₂ be the values that you specify for the lower limit and the upper limit, respectively. By default, the lower equivalence limit, δ₁, is given by:

and the upper equivalence limit, δ₂, is given by:

However, if you select the option to multiply your limits by the target value, then the limits are given by:

Degrees of freedom (DF)

Notation

Term	Description
v	Degrees of freedom
n	Number of observations

Confidence interval for the difference

100(1 – α)% CI

By default, Minitab uses the following formula to calculate the 100(1 – α)% confidence interval (CI) for the difference:

CI = [min(C, D_l), max(C, D_u)]

where:

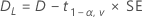
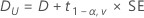
100(1 – 2α)% CI

If you select the option to use the 100(1 – 2 α)% CI, then the CI is given by the following formula:

CI = [D_l, D_u]

One-sided intervals

For a hypotheses of Test mean > target, or Test mean - target > lower limit, the 100(1 – α)% lower bound is equal to D_L.

For a hypothesis of Test mean < target, or Test mean - target < upper limit, the 100(1 – α)% upper bound is equal to D_U.

Notation

Term	Description
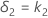
D	Difference between the mean of the test sample and the target value
SE	Standard error
δ₁	Lower equivalence limit
δ₂	Upper equivalence limit
v	Degrees of freedom
α	Significance level for the test
t_{1 – α, v}	Upper 1 – α critical value for a t-distribution with v degrees of freedom

T-values

Let t ₁ be the t-value for the hypothesis,

, and let t ₂ be the t-value for the hypothesis,

, where

is the difference between the mean of the test population and the target value. By default, the t-values are calculated as follows:

For a hypothesis of Test mean > target, δ₁= 0.

For a hypothesis of Test mean < target, δ₂= 0.

Notation

Term	Description
D	Difference between the mean of the test sample and the target value
SE	Standard error of the difference
δ₁	Lower equivalence limit
δ₂	Upper equivalence limit

P-values

The probability, P_H₀, for each null hypothesis (H₀) is given by the following:

H₀	P-Value

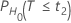Notation

Term	Description
	Unknown difference between the mean of the test population and the target value
δ₁	Lower equivalence limit
δ₂	Upper equivalence limit
v	Degrees of freedom
T	t distribution with v degrees of freedom
t₁	The t-value for the hypothesis
t₂	The t- value for the hypothesis

Note

For information on how the t-values are calculated, see the section on t-values.