A packaging engineer wants to test a new method to seal snack bags. The force that is required to open the bags should be within 10% of the target value of 4.2 N (Newtons). The engineer randomly samples 28 bags that are sealed using the new method and records the force that is required to open each bag.
The engineer performs a 1-sample equivalence test to determine whether the mean force that is required to open bags with the new seal is within 10% of the target of 4.2 N.
- Open the sample data, SnackBagSeal.MWX.
- Choose .
- From the drop-down list, select Sample in a column.
- In Sample, enter Force.
- In Target, enter 4.2.
- From What do you want to determine? (Alternative hypothesis), select Lower limit < test mean - target < upper limit.
- In Lower limit, enter –0.1.
- In Upper limit, enter 0.1.
- Select Multiply by target.
- Click OK.
Interpret the results
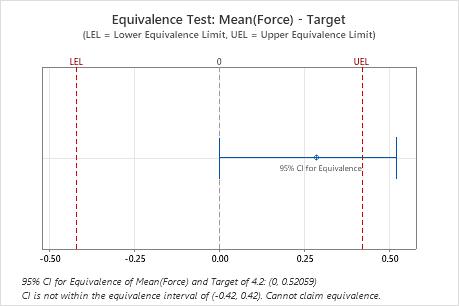
The confidence interval is not completely within the equivalence interval. Therefore, the engineer cannot claim that the force that is required to open the bags with the new seal is equivalent to the target of 4.2 N.
Method
Lower equivalence limit = -0.1 × target = -0.42
Upper equivalence limit = 0.1 × target = 0.42
Descriptive Statistics
| Variable | N | Mean | StDev | SE Mean |
|---|---|---|---|---|
| Force | 28 | 4.4850 | 0.73188 | 0.13831 |
Difference: Mean(Force) - Target
| Difference | SE | 95% CI for Equivalence | Equivalence Interval |
|---|---|---|---|
| 0.28500 | 0.13831 | (0, 0.520586) | (-0.42, 0.42) |
Test
| Null hypothesis: | Difference ≤ -0.42 or Difference ≥ 0.42 |
|---|---|
| Alternative hypothesis: | -0.42 < Difference < 0.42 |
| α level: | 0.05 |
| Null Hypothesis | DF | T-Value | P-Value |
|---|---|---|---|
| Difference ≤ -0.42 | 27 | 5.0972 | 0.000 |
| Difference ≥ 0.42 | 27 | -0.97605 | 0.169 |