In This Topic
Step 1: Determine a confidence interval for the population mean difference
First, consider the mean difference, and then examine the confidence interval. The mean difference is the average of the differences between the paired observations in your sample.
The mean difference is an estimate of the population mean difference. Because the mean difference is based on sample data and not on the entire population, it is unlikely that the sample mean difference equals the population mean difference. To better estimate the population mean difference, use the confidence interval of the difference.
The confidence interval provides a range of likely values for the population mean difference of the paired observations. For example, a 95% confidence level indicates that if you take 100 random samples from the population, you could expect approximately 95 of the samples to produce intervals that contain the population mean difference. The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size. For more information, go to Ways to get a more precise confidence interval.
Estimation for Paired Difference
| Mean | StDev | SE Mean | 95% CI for μ_difference |
|---|---|---|---|
| 2.200 | 3.254 | 0.728 | (0.677, 3.723) |
Key Results: Mean Difference, 95% CI for mean difference
In these results, the estimate for the population mean difference in heart rates is 2.2. You can be 95% confident that the population mean difference is between 0.677 and 3.723.
Step 2: Determine whether the test results are statistically significant
- P-value ≤ α: The difference between the means is statistically significant (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis. You can conclude that the difference between the population means does not equal the hypothesized difference. If you did not specify a hypothesized difference, Minitab tests whether there is no difference between the means (Hypothesized difference = 0) Use your specialized knowledge to determine whether the difference is practically significant. For more information, go to Statistical and practical significance.
- P-value > α: The difference between the means is not statistically significant (Fail to reject H0)
- If the p-value is greater than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that the mean difference between the paired observations is statistically significant. You should make sure that your test has enough power to detect a difference that is practically significant. For more information, go to Power and Sample Size for Paired t.
Test
| Null hypothesis | H₀: μ_difference = 0 |
|---|---|
| Alternative hypothesis | H₁: μ_difference ≠ 0 |
| T-Value | P-Value |
|---|---|
| 3.02 | 0.007 |
Key Result: P-Value
In these results, the null hypothesis states that the mean difference in resting heart rates for patients before and after a running program is 0. Because the p-value is 0.007, which is less than the significance level of 0.05, the decision is to reject the null hypothesis and conclude that there is a difference in the heart rates for patients before and after a running program.
Step 3: Check your data for problems
Problems with your data, such as skewness and outliers, can adversely affect your results. Use graphs to look for skewness and to identify potential outliers.
Examine the spread of your data to determine whether your data appear to be skewed.
When data are skewed, the majority of the data are located on the high or low side of the graph. Often, skewness is easiest to detect with a histogram or boxplot.
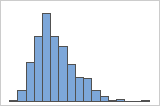
Right-skewed
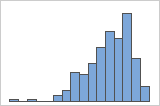
Left-skewed
The histogram with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The histogram with left-skewed data shows failure time data. A few items fail immediately, and many more items fail later.
Data that are severely skewed can affect the validity of the p-value if your sample is small (less than 20 values). If your data are severely skewed and you have a small sample, consider increasing your sample size.
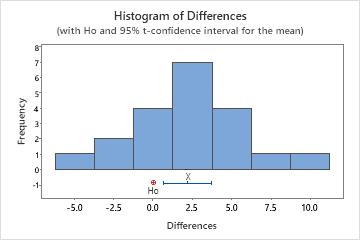
In this histogram, the data do not appear to be severely skewed.
Identify outliers
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
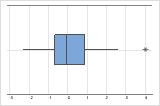
On a boxplot, asterisks (*) denote outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
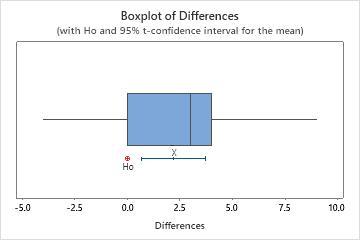
In this boxplot, there are no outliers.
